
分析 (Ⅰ)先求导,利用导数求出函数最小值即可,
(Ⅱ)利用分析法,要证f(x0)<a<y0,只需证${e^{\frac{t}{2}}}-{e^{-\frac{t}{2}}}>t$,构造函数$F(t)={e^{\frac{t}{2}}}-{e^{-\frac{t}{2}}}-t$,利用导数只需证明$\frac{{{e^t}-1}}{{{e^t}+1}}<\frac{t}{2}$,再构造函数,根据导数和函数的单调性的关系即可证明
解答 解:(Ⅰ)h(x)=ex-ax-b,求导得h'(x)=ex-a
当a≤0时,h'(x)>0,h(x)在R上为增函数,不满足有两个零点,故不合题意;
所以a>0,令h'(x)=0,解得x=lna,
并且有x∈(-∞,lna),h'(x)<0;x∈(lna,+∞),h'(x)>0,
故$h{(x)_{min}}=h(lna)={e^{lna}}-alna-b=a-b-alna$.
(Ⅱ)证明:要证f(x0)<a<y0成立,
即证${e^{\frac{{{x_1}+{x_2}}}{2}}}<\frac{{{e^{x_2}}-{e^{x_1}}}}{{{x_2}-{x_1}}}<\frac{{{e^{x_2}}+{e^{x_1}}}}{2}$,不妨设x2>x1,
只需证${e^{\frac{{{x_2}-{x_1}}}{2}}}<\frac{{{e^{{x_2}-{x_1}}}-1}}{{{x_2}-{x_1}}}<\frac{{{e^{{x_2}-{x_1}}}+1}}{2},令t={x_2}-{x_1}>0$,
即为${e^{\frac{t}{2}}}<\frac{{{e^t}-1}}{t}<\frac{{{e^t}+1}}{2}$,
要证${e^{\frac{t}{2}}}<\frac{{{e^t}-1}}{t}$,只需证${e^{\frac{t}{2}}}-{e^{-\frac{t}{2}}}>t$,
令$F(t)={e^{\frac{t}{2}}}-{e^{-\frac{t}{2}}}-t$,
只需证F(t)>0,求导$F'(t)=\frac{1}{2}{e^{\frac{t}{2}}}+\frac{1}{2}{e^{-\frac{1}{2}}}-1=\frac{1}{2}({e^{\frac{t}{2}}}+{e^{-\frac{t}{2}}})-1>0$,
∴F(t)在(0,+∞)为增函数,
故F(t)>F(0)=0,
∴${e^{\frac{t}{2}}}<\frac{{{e^t}-1}}{t}成立$;
要证$\frac{{{e^t}-1}}{t}<\frac{{{e^t}+1}}{2}$,
只需证明$\frac{{{e^t}-1}}{{{e^t}+1}}<\frac{t}{2}$,
令$G(t)=\frac{{{e^t}-1}}{{{e^t}+1}}-\frac{t}{2}$,
求导$G'(t)=\frac{{2{e^t}}}{{{{({e^t}+1)}^2}}}-\frac{1}{2}=\frac{{4{e^t}-{{({e^t}+1)}^2}}}{{2{{({e^t}+1)}^2}}}=\frac{{-{{({{e^t}-1})}^2}}}{{2{{({{e^t}+1})}^2}}}<0$,
∴G(t)在(0,+∞)为减函数,故G(t)<G(0)=0,
∴${e^{\frac{t}{2}}}<\frac{{{e^t}-1}}{t}成立$;
∴${e^{\frac{t}{2}}}<\frac{{{e^t}-1}}{t}<\frac{{{e^t}+1}}{2}$,t>0,成立,
∴f(x0)<a<y0成立.
点评 本题考查不等式的证明,利用导数研究函数的最值,考查分类整合思想、转化思想,考查学生综合运用知识分析解决问题的能力,属于难题


科目:高中数学 来源: 题型:选择题
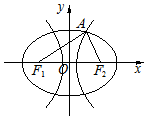 如图,椭圆与双曲线有公共焦点F1,F2,它们在第一象限的交点为A,且AF1⊥AF2
如图,椭圆与双曲线有公共焦点F1,F2,它们在第一象限的交点为A,且AF1⊥AF2| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | A1 | A2 | A3 | A4 | A5 |
| 评价指数(x,y,z) | (3,4,3) | (4,3,4) | (4,4,2) | (4,3,5) | (4,5,4) |
| 学生编号 | B1 | B2 | B3 | B4 | B5 |
| 评价指数(x,y,z) | (3,5,3) | (4,3,2) | (5,4,4) | (5,4,5) | (4,5,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})∪({2{e^{\frac{3}{2}}},+∞})$ | B. | $({-∞,\frac{1}{2}})∪({4{e^{\frac{3}{2}}},+∞})$ | C. | $({-∞,2{e^{\frac{3}{2}}}})$ | D. | $({-∞,1})∪({4{e^{\frac{3}{2}}},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com