
| A. | (-∞,1) | B. | (-∞,2) | C. | (-2,+∞) | D. | (2,+∞) |
分析 由已知当x<0时,f(x)=$\left\{\begin{array}{l}{-ax+lo{g}_{5}(-x),x<-4}\\{{x}^{2}+{2}^{-x}+3,-4≤x<0}\end{array}\right.$,从而f(-5)=5a+1,f(2)=11,由此利用f(-5)<f(2),能求出a的取值范围.
解答 解:∵f(x)是定义在R上的偶函数,当x>0时,f(x)=$\left\{\begin{array}{l}{ax+lo{g}_{5}x,}&{x>4}\\{{x}^{2}+{2}^{x}+3,}&{0<x≤4}\end{array}\right.$,
∴当x<0时,f(x)=$\left\{\begin{array}{l}{-ax+lo{g}_{5}(-x),x<-4}\\{{x}^{2}+{2}^{-x}+3,-4≤x<0}\end{array}\right.$,
∴f(-5)=5a+1,f(2)=4+4+3=11,
∵f(-5)<f(2),
∴5a+1<11,解得a<2.
∴a的取值范围为(-∞,2).
故选:B.
点评 本题考查实数取值范围的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知y=f(x)是定义在R上的奇函数,且x<0时,f(x)=1+2x.
(1)求函数f(x)的解析式.
(2)画出函数f(x)的图象.
(3)写出函数f(x)单调区间及值域.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=0 | B. | |$\overrightarrow{AB}$+$\overrightarrow{AC}$|≥2|$\overrightarrow{AD}$| | C. | $\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|2 | D. | $\overrightarrow{AC}$•$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$=|$\overrightarrow{AB}$|sinB |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
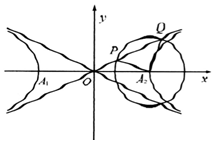 如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com