
| A. | $\sqrt{13}$ | B. | 13 | C. | 5 | D. | 2$\sqrt{13}$ |
分析 过点O分别作OE⊥AB于E,OF⊥AC于F,可得E、F分别是AB、AC的中点.根据Rt△AOE中余弦的定义,分别求出$\overrightarrow{AB}$•$\overrightarrow{AO}$,$\overrightarrow{AC}$•$\overrightarrow{AO}$的值,再由M是BC边的中点,得到$\overrightarrow{AM}$•$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{AO}$,问题得以解决.
解答 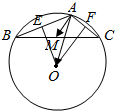 解:过点O分别作OE⊥AB于E,OF⊥AC于F,则E、F分别是AB、AC的中点
解:过点O分别作OE⊥AB于E,OF⊥AC于F,则E、F分别是AB、AC的中点
可得Rt△AEO中,cos∠OAE=$\frac{|\overrightarrow{AE}|}{|\overrightarrow{AO}|}$=$\frac{|\overrightarrow{AB|}}{2|\overrightarrow{AO}|}$,
∴$\overrightarrow{AB}$•$\overrightarrow{AO}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AO}$|•$\frac{|\overrightarrow{AB|}}{2|\overrightarrow{AO}|}$=$\frac{1}{2}$|$\overrightarrow{AB}$|2=18,
同理可得$\overrightarrow{AC}$•$\overrightarrow{AO}$=$\frac{1}{2}$|$\overrightarrow{AC}$|2=8,
∵M是边BC的中点,$\overrightarrow{AM}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)
∴$\overrightarrow{AM}$•$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$•$\overrightarrow{AO}$+$\overrightarrow{AC}$•$\overrightarrow{AO}$)=$\frac{1}{2}$(18+8)=13,
故选:B.
点评 本题主要考查平面向量数量积的应用,着重考查了平面向量的数量积的运算性质和三角形外接圆等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-2}{4}$ | B. | $\frac{π}{2}$-4 | C. | $\frac{π-1}{4}$ | D. | $\frac{π-4}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
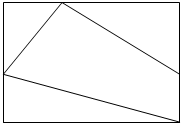 用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )
用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )| A. | 180 | B. | 240 | C. | 160 | D. | 320 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com