
【题目】选修4-4:坐标系与参数方程.
在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ; 线
; 线![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)直线![]() 的参数方程中的参数为
的参数方程中的参数为![]() ,所以消
,所以消![]() 得到直线的普通方程;根据
得到直线的普通方程;根据![]() ,
,![]() ,极坐标方程两边同时乘以
,极坐标方程两边同时乘以![]() ,化简为曲线
,化简为曲线![]() 的普通方程;(2)根据直线
的普通方程;(2)根据直线![]() 过点
过点![]() ,可知直线的倾斜角,代入直线的参数方程,得到
,可知直线的倾斜角,代入直线的参数方程,得到![]()
 ,代入曲线
,代入曲线![]() 的极坐标方程,转化为关于
的极坐标方程,转化为关于![]() 的一元二次方程,根据
的一元二次方程,根据![]() 的几何意义可知
的几何意义可知![]() .
.
试题解析:(1)∵直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
∴直线![]() 的普通方程为
的普通方程为![]() ....................2分
....................2分
由![]() ,得
,得![]() ,即
,即![]() ,
,
∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .............................4分
.............................4分
(2)∵点![]() 的极坐标为
的极坐标为![]() ,∴点
,∴点![]() 的直角坐标为
的直角坐标为![]() ...............5分
...............5分
∴![]() ,直线
,直线![]() 的倾斜角
的倾斜角![]() .
.
∴直线![]() 的参数方程为
的参数方程为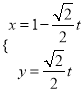 (
(![]() 为参数)...................7分
为参数)...................7分
代入![]() ,得
,得![]() .....................8分
.....................8分
设![]() 两点对应的参数为
两点对应的参数为![]() .
.
∵![]() 为线段
为线段![]() 的中点,
的中点,
∴点![]() 对应的参数值为
对应的参数值为![]() .
.
又点![]() ,则
,则![]() .........................10分
.........................10分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.

(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x∈R|2x﹣8=0},B={x∈R|x2﹣2(m+1)x+m2=0}
(1)若m=4,求A∪B;
(2)若A∪B=A,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3log
的等比数列,设bn+2=3log ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() +m﹣1对一切正整数n恒成立,求实数m的取值范围.
+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
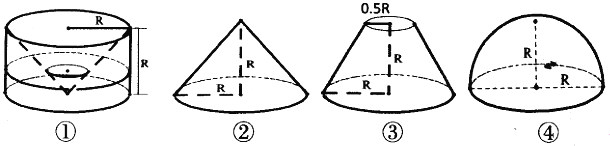
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x2﹣2ax﹣b,其中a,b是实数.
(1)若不等式f(x)≤0的解集是[0,6],求ab的值;
(2)若b=3a,对任意x∈R,都有f(x)≥0,且存在实数x,使得f(x)≤2﹣ ![]() a,求实数a的取值范围;
a,求实数a的取值范围;
(3)若方程有一个根是1,且a,b>0,求 ![]() 的最小值,及此时a,b的值.
的最小值,及此时a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com