给出下列命题: ①如果函数f(x)对任意的.都有f (a为一个常数).那么函数f(x)必为偶函数, ②如果函数f(x)对任意的.满足f.那么函数是周期函数, ③如果函数f(x)对任意的且x1≠x2.都有(x1-x2)[f(x1)-f(x2)]＞0.那么函数f(x)在R上是增函数, ④函数y＝f+2的图象一定不能重合．其中真命题的序号是 [ ] A．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

给出下列命题：

①如果函数f(x)对任意的，都有f(a＋x)＝f(a－x) (a为一个常数)，那么函数f(x)必为偶函数；

②如果函数f(x)对任意的，满足f(2＋x)＝－f(x)，那么函数是周期函数；

③如果函数f(x)对任意的且x₁≠x₂，都有(x₁－x₂)[f(x₁)－f(x₂)]＞0，那么函数f(x)在R上是增函数；

④函数y＝f(x)和函数y＝f(x－1)＋2的图象一定不能重合．

其中真命题的序号是

[　　]

A．①④

B．②③

C．①②③

D．②③④

答案：B

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

10、如图，平面中两条直线l₁和l₂相交于点O，对于平面上任意一点M，若p、q分别是M到直线l₁和l₂的距离，则称有序非负实数对（p，q）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列命题：
①若p=q=0，则“距离坐标”为（0，0）的点有且仅有1个；
②若pq=0，且p+q≠0，则“距离坐标”为（p，q）的点有且仅有2个；
③若pq≠0，则“距离坐标”为（p，q）的点有且仅有4个．
上述命题中，正确命题的个数是（　　）

A、0

B、1

C、2

D、3

查看答案和解析>>

科目：高中数学 来源： 题型：

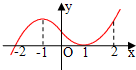如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
①-2是函数y=f（x）的极值点；
②1是函数y=f（x）的最小值点；
③y=f（x）在x=0处切线的斜率小于零；
④y=f（x）在区间（-2，2）上单调递增．
则正确命题的序号是

①④

．

查看答案和解析>>

科目：高中数学 来源： 题型：

如图展示了一个由区间（0，1）到实数集R的映射过程：区间（0，1）中的实数m对应数轴上的点M，如图①；将线段AB围成一个圆，使两端点A、B恰好重合，如图②；再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1），在图形变化过程中，图①中线段AM的长度对应于图③中的弧ADM的长度，如图③．图③中直线AM与x轴交于点N（n，0），则m的象就是n，记作f（m）=n．

给出下列命题：①f（

）=1；②f（x）是奇函数；③f（x）在定义域上单调递增，则所有真命题的序号是

③

．（填出所有真命题的序号）

查看答案和解析>>

科目：高中数学 来源： 题型：

如图，四面体OABC的三条棱OA、OB、OC两两垂直，OA=OB=2，OC=3，D为四面体OABC外一点．给出下列命题．
①不存在点D，使四面体ABCD有三个面是直角三角形
②不存在点D，使四面体ABCD是正三棱锥
③存在点D，使CD与AB垂直并且相等
④存在无数个点D，使点O在四面体ABCD的外接球面上
其中真命题的序号是

③④

．

查看答案和解析>>

科目：高中数学 来源： 题型：

（2011•洛阳二模）给出下列命题：
①设向量

，

满足|

|=2，|

|=1，

，

的夹角为

．若向量2t

与

的夹角为钝角，则实数t的取值范围是（-7，-

）；
②已知一组正数x₁，x₂，x₃，x₄的方差为s²=

（x₁²+x₂²+x₃²+x₄²）-4，则x₁+1，x₂+1，x₃+1，x₄+1的平均数为1
③设a，b，c分别为△ABC的角A，B，C的对边，则方程x²+2ax+b²=o与x²+2cx-b²=0有公共根的充要条件是A=90°；
④若f（n）表示n²+1（n∈N）的各位上的数字之和，如11²+1=122，1+2+2=5，所以f（n）=5，记f₁（n）=f（n），f₂（n）=f[f₁（n）]，…f_k+1（n）=f[f_k（n）]，k∈N，则f₂₀（5）=11．
上面命题中，假命题的序号是

②

（写出所有假命题的序号）．

查看答案和解析>>

同步练习册答案