
分析 根据x5+3x3+1=[1+(x-1)]5+3[1+(x-1)]3+1,按照二项式定理展开,和所给的等式作对比,求得a3的值
解答 解:∵函数f(x)=1+3x5-2x7=1+3[(x-1)+1]5-2[(x-1)+1]7
=1+3-2+(3${C}_{5}^{4}$-2${C}_{7}^{6}$)(x-1)+(3${C}_{5}^{3}$-2${C}_{7}^{5}$)•(x-1)2+(3${C}_{5}^{2}$-2${C}_{7}^{4}$)•(x-1)3+…-2${C}_{7}^{0}$•(x-1)7,
又f(x)=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,
∴a2=3${C}_{5}^{3}$-2${C}_{7}^{5}$=30-42=-12,
故答案为:-12.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{-1+\sqrt{3}}}{2}$ | B. | $\frac{{-1+\sqrt{5}}}{2}$ | C. | $\frac{{1+\sqrt{5}}}{2}$ | D. | $2+\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
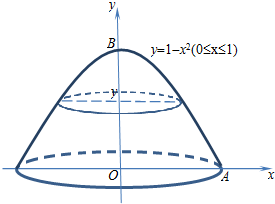 在xOy平面上,将抛物线弧y=1-x2(0≤x≤1)、x轴、y轴围成的封闭图形记为D,如图中曲边三角形OAB及内部.记D绕y轴旋转一周而成的几何体为Ω,过点(0,y)(0≤y≤1)作Ω的水平截面,所得截面面积为(1-y)π,试构造一个平放的直三棱柱,利用祖暅原理得出Ω的体积值为$\frac{π}{2}$.
在xOy平面上,将抛物线弧y=1-x2(0≤x≤1)、x轴、y轴围成的封闭图形记为D,如图中曲边三角形OAB及内部.记D绕y轴旋转一周而成的几何体为Ω,过点(0,y)(0≤y≤1)作Ω的水平截面,所得截面面积为(1-y)π,试构造一个平放的直三棱柱,利用祖暅原理得出Ω的体积值为$\frac{π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com