
分析 (1)利用同角三角函数的基本关系式求解即可.
(2)利用诱导公式化简表达式然后求解函数值即可.
解答 解:(1)sinα=-$\frac{4}{5}$且$\frac{π}{2}$<α<$\frac{3π}{2}$.
cosα=-$\sqrt{1-{sin}^{2}α}$=-$\frac{3}{5}$;
(2)$\frac{sin(\frac{π}{2}-α)cos(-α-π)tan(π-α)}{sin(-π+α)cos(\frac{π}{2}+α)}$
=$\frac{cosαcosαtanα}{sinαsinα}$
=$\frac{cosα}{sinα}$
=$\frac{-\frac{3}{5}}{-\frac{4}{5}}$
=$\frac{3}{4}$.
点评 本题考查三角函数的化简求值,诱导公式的应用,考查计算能力.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.
在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
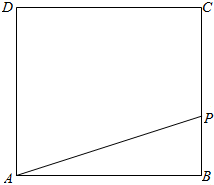 分别根据下列两个实际背景
分别根据下列两个实际背景查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com