
已知各项都为正的等比数列{an}满足a7=a6+2a5,存在两项am,an使得 =4a1,则
=4a1,则 的最小值为( ).
的最小值为( ).
A. B.
B. C.
C.  D.
D.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:填空题
已知点F是双曲线 =1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.
=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=2,∠BAD=60°.

(1)求证:OM∥平面PAB;
(2)求证:平面PBD⊥平面PAC;
(3)当四棱锥P-ABCD的体积等于 时,求PB的长.
时,求PB的长.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:选择题
某四棱台的三视图如图所示,则该四棱台的体积是( ).
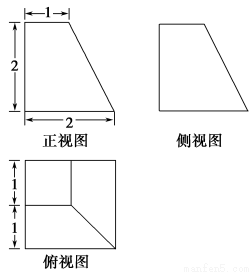
A.4 B. 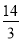 C.
C.  D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:填空题
设Sn为数列{an}的前n项和,若 (n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
(n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,椭圆C: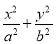 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为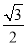 ,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
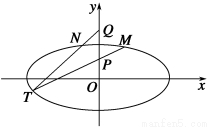
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2),设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T.求证:点T在椭圆C上.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:选择题
已知点P(x,y)是直线kx+y+4=0(k>0)上一动点,PA,PB是圆C:x2+y2-2y=0的两条切线,A,B为切点,若四边形PACB的最小面积是2,则k的值为( ).
A.4 B.3 C.2 D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:选择题
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是( ).
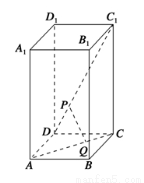
A. B.
B. 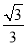 C.
C. 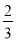 D.
D.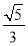
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:填空题
小王参加人才招聘会,分别向A,B两个公司投递个人简历.假定小王得到A公司面试的概率为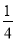 ,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=
,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=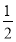 ,则随机变量X的数学期望为________.
,则随机变量X的数学期望为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com