
分析 若在四个半径为1且两两相切的实心小球所形成的球间空隙内放置一个与其它球都相切的小球,可先求出该球的半径,若将一个棱长为a的正方体嵌入到四个半径为1且两两相切的实心小球所形成的球间空隙内,使得正方体能够任意自由地转动,则$\sqrt{3}$a=2r,进而可得答案.
解答 解:若在四个半径为1且两两相切的实心小球所形成的球间空隙内放置一个与其它球都相切的小球,
设该小球的半径为r,
则r+1+$\sqrt{(r+1)^{2}-(\frac{2\sqrt{3}}{3})^{2}}$=$\frac{2\sqrt{6}}{3}$,
解得:r=$\frac{\sqrt{6}-2}{2}$,
若将一个棱长为a的正方体嵌入到四个半径为1且两两相切的实心小球所形成的球间空隙内,使得正方体能够任意自由地转动,
则:$\sqrt{3}$a=2r,
解得:a=$\frac{{3\sqrt{2}-2\sqrt{3}}}{3}$,
故答案为:$\frac{{3\sqrt{2}-2\sqrt{3}}}{3}$.
点评 本题考查的知识点是空间球与球之间的位置关系,正三棱锥的高与棱长的关系,难度较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
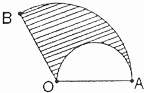 如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )| A. | $\frac{5}{8π}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{8π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$-2 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 科目 学生人数 | A | B | C |
| 120 | 是 | 否 | 是 |
| 60 | 否 | 否 | 是 |
| 70 | 是 | 是 | 否 |
| 50 | 是 | 是 | 是 |
| 150 | 否 | 是 | 是 |
| 50 | 是 | 否 | 否 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-1-5i}{2}$ | B. | $\frac{1+5i}{2}$ | C. | $\frac{1-5i}{2}$ | D. | $\frac{-1+5i}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com