
分析 根据题意,利用诱导公式与同角的三角函数关系,即可求出sin($\frac{π}{6}$+α)的值.
解答 解:∵sin($\frac{π}{3}$-α)=$\frac{1}{3}$,
∴cos($\frac{π}{6}$+α)=cos[$\frac{π}{2}$-($\frac{π}{3}$-α)]=sin($\frac{π}{3}$-α);
又0<α<$\frac{π}{2}$,∴$\frac{π}{6}$<$\frac{π}{6}$+α<$\frac{2π}{3}$,
∴sin($\frac{π}{6}$+α)=$\sqrt{1{-cos}^{2}(\frac{π}{6}+α)}$=$\sqrt{1{-(\frac{1}{3})}^{2}}$=$\frac{2\sqrt{2}}{3}$.
故答案为:$\frac{2\sqrt{2}}{3}$.
点评 本题考查了诱导公式与同角三角函数关系的应用问题,是基础题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
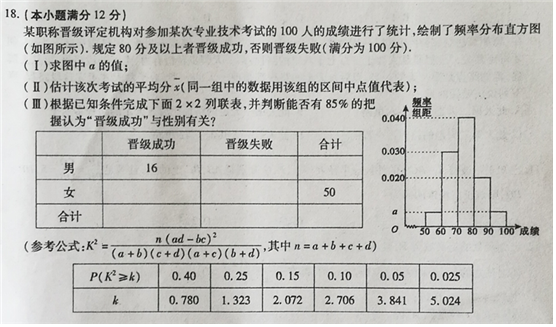
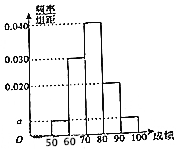 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
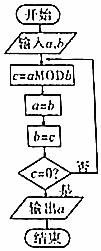 “欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )| A. | 0 | B. | 25 | C. | 50 | D. | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 公元263年左右,我国数学家刘徽发现,当圆内接正多边形的边数无限增加时,正多边形的周长可无限逼近圆的周长,并创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率,利用刘徽的割圆术设计的程序框图如图所示,若输出的n=96,则判断框内可以填入( )(参考数据:sin7.5°≈0.1305,sin3.75°≈0.06540,sin1.875°≈0.03272)
公元263年左右,我国数学家刘徽发现,当圆内接正多边形的边数无限增加时,正多边形的周长可无限逼近圆的周长,并创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率,利用刘徽的割圆术设计的程序框图如图所示,若输出的n=96,则判断框内可以填入( )(参考数据:sin7.5°≈0.1305,sin3.75°≈0.06540,sin1.875°≈0.03272)| A. | p≤3.14 | B. | p≥3.14 | C. | p≥3.1415 | D. | p≥3.1415926 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com