
【题目】已知正方体ABCD﹣A1B1C1D1 , 则AC与平面BDC1所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:以A1为原点建立如图所示的空间直角坐标系,
∵A1A⊥平面ABCD,∴A1A⊥BD,
又BD⊥AC,A1A与AC为平面A1AC内的相交直线,
∴BD⊥平面A1AC,
∴BD⊥A1C,
同理可证:BC1⊥A1C,
∴A1C⊥平面BDC1 , ∴ ![]() 是平面BDC1的一个法向量,
是平面BDC1的一个法向量,
设正方体棱长为1,
则 ![]() =(1,1,1),
=(1,1,1), ![]() =(1,1,0),
=(1,1,0), ![]() =2,|
=2,| ![]() |=
|= ![]() ,|
,| ![]() |=
|= ![]() ,
,
∴cos< ![]() ,
, ![]() >=
>= 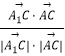 =
= ![]() ,
,
设AC与平面BDC1所成角为α,则sinα= ![]() ,∴cosα=
,∴cosα= ![]() .
.
故选:B.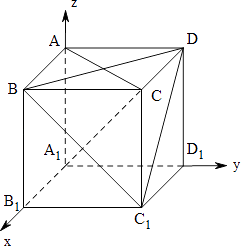
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则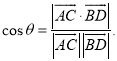 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,N为CD1中点,M为线段BC1上的动点,(M不与B,C1重合)有四个命题:
①CD1⊥平面BMN;
②MN∥平面AB1D1;
③平面AA1CC1⊥平面BMN;
④三棱锥D﹣MNC的体积有最大值.
其中真命题的序号是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x .
(1)解方程f(log4x)=3;
(2)已知不等式f(x+1)≤f[(2x+a)2](a>0)对x∈[0,15]恒成立,求实数a的取值范围;
(3)存在x∈(﹣∞,0],使|af(x)﹣f(2x)|>1成立,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为D,值域为A,如果存在函数x=g(t),使得函数y=f[g(t)]的值域仍是A,那么称x=g(t)是函数y=f(x)的一个等值域变换.
(1)判断下列函数x=g(t)是不是函数y=f(x)的一个等值域变换?说明你的理由; ① ![]() ;
;
②f(x)=x2﹣x+1,x∈R,x=g(t)=2t , t∈R.
(2)设f(x)=log2x的定义域为x∈[2,8],已知 ![]() 是y=f(x)的一个等值域变换,且函数y=f[g(t)]的定义域为R,求实数m、n的值.
是y=f(x)的一个等值域变换,且函数y=f[g(t)]的定义域为R,求实数m、n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是抛物线y2=4x上的一个动点,则点P到直线l1:3x﹣4y+12=0和l2:x+2=0的距离之和的最小值是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a3=12,a11=﹣5,且任意连续三项的和均为11,则a2017=;设Sn是数列{an}的前n项和,则使得Sn≤100成立的最大整数n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(2a+1)x+b,其中a,b∈R. (Ⅰ)当a=1,b=﹣4时,求函数f(x)的零点;
(Ⅱ)如果函数f(x)的图象在直线y=x+2的上方,证明:b>2;
(Ⅲ)当b=2时,解关于x的不等式f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件样本,测量这些样本的一项质量指标值,由测量结果得如下频数分布表:
质量指标 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
频数 | 6 | 26 | 38 | 22 | 8 |
则样本的该项质量指标值落在[105,125]上的频率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点. 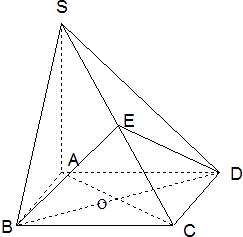
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
(3)设SA=4,AB=2,当OE丄SC时,求二面角E﹣BD﹣C余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com