
分析 (1)利用an+1=Sn+1-Sn可知证明an+1=4(an-an-1),通过bn=an+1-2an可知bn+1=2(an+1-2an),通过作商可知{bn}是公比为2的等比数列,通过a1=1可知b1=3,进而可得结论;
(2)通过(1)可知cn=2n-1,裂项可知$\frac{1}{lo{g}_{2}{C}_{n+2}•lo{g}_{2}{C}_{n+1}}$=$\frac{1}{n}$-$\frac{1}{n+1}$,并项相加即得结论.
解答 (1)证明:an+1=Sn+1-Sn=(4an+2)-(4an-1+2)
=4(an-an-1) (n∈N+,n≥2).…(1分)
由题意知bn=an+1-2an,
∴bn+1=an+2-2an+1.
∴bn+1=4(an+1-an)-2an+1=2an+1-4an=2(an+1-2an),…(3分)
∴$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{2({a}_{n-1}-2{a}_{n})}{{a}_{n-1}-2{a}_{n}}$=2(n∈N+),
∴{bn}是等比数列,公比q=2.…(5分)
又∵S2=4a1+2,∴a1+a2=4a1+2,
∴1+a2=4+2,∴a2=5,
∴b1=a2-2a1=5-2=3,
∴bn=b1•qn-1=3•2n-1.…(7分)
(2)解:∵cn=$\frac{{b}_{n}}{3}$=2n-1,…(8分)
∴$\frac{1}{lo{g}_{2}{C}_{n+2}•lo{g}_{2}{C}_{n+1}}$=$\frac{1}{(n+1)n}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴Tn=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.…(10分)
点评 本题考查数列的通项及前n项和,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:选择题
| A. | 至少有一个白球;都是白球 | B. | 至少有一个白球;至少有一个红球 | ||
| C. | 至少有一个白球;红球、黑球各一个 | D. | 恰有一个白球;白球、黑球各一个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
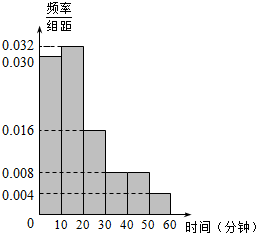 某校决定为本校上学时间不少于30分钟的学生提供校车接送服务.为了解学生上学所需时间,从全校600名学生中抽取50人统计上学时间(单位:分钟),现对600人随机编号为001,002,…600.抽取50位学生上学时间均不超过60分钟,将时间按如下方式分成六组,第一组上学时间在[0,10),第二组上学时间在[10,20),…第六组上学时间在[50,60]得到各组人数的频率分布直方图.如图.
某校决定为本校上学时间不少于30分钟的学生提供校车接送服务.为了解学生上学所需时间,从全校600名学生中抽取50人统计上学时间(单位:分钟),现对600人随机编号为001,002,…600.抽取50位学生上学时间均不超过60分钟,将时间按如下方式分成六组,第一组上学时间在[0,10),第二组上学时间在[10,20),…第六组上学时间在[50,60]得到各组人数的频率分布直方图.如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<-1或b>1 | B. | -1<b<1 | C. | b>1 | D. | b>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com