
分析 先设木棒其中两段的长度分别为x、y,分别表示出木棒随机地折成3段的x,y的约束条件和3段构成三角形的约束条件,再画出约束条件表示的平面区域,利用面积测度即可求出构成三角形的概率.
解答 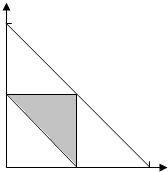 解:不妨设这条线段的长为l=1.设三段长分别为x,y,1-x-y,
解:不妨设这条线段的长为l=1.设三段长分别为x,y,1-x-y,
则总样本空间为$\left\{\begin{array}{l}{0<x<1}\\{0<y<1}\\{x+y<1}\end{array}\right.$,
其面积为$\frac{1}{2}$,
能构成三角形的事件的空间为$\left\{\begin{array}{l}{x+y>1-x-y}\\{x+1-x-y>y}\\{y+1-x-y>x}\end{array}\right.$,即$\left\{\begin{array}{l}{x+y>\frac{1}{2}}\\{y<\frac{1}{2}}\\{x<\frac{1}{2}}\end{array}\right.$
其面积为$\frac{1}{8}$,
则所求概率为$\frac{1}{4}$.
点评 本题主要考查了几何概型,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com