
分析 问题转化为lnx<x($\frac{1+a}{2}$x-a)在x∈(1,+∞)恒成立,令p(x)=lnx,q(x)=x($\frac{1+a}{2}$x-a),结合函数图象求出a的范围即可.
解答 解:当x∈(1,+∞)时,f(x)>g(x)恒成立,
即lnx<x($\frac{1+a}{2}$x-a)在x∈(1,+∞)恒成立,
令p(x)=lnx,q(x)=x($\frac{1+a}{2}$x-a),
画出函数p(x),q(x)图象,如图示: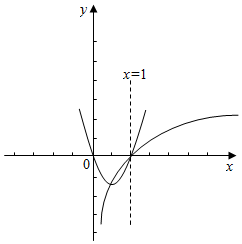 ,
,
结合图象q(x)开口向上,故$\frac{a+1}{2}$>0,解得:a>-1,
且x=$\frac{2a}{1+a}$<1,解得:a<1,
故-1<a<1.
点评 本题考查了二次函数、对数函数的性质,考查数形结合思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.
某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
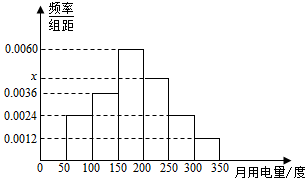 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示,在这些用户中,用电量落在区间[150,250)内的户数为52.
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示,在这些用户中,用电量落在区间[150,250)内的户数为52.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com