
分析 (1)通过对5(a1+a2)=a1+a2+a3+a4化简可知公比q=2,进而可知数列{an}的通项与前n项和;
(2)通过(1)裂项可知$\frac{{a}_{n}}{{S}_{n}{S}_{n+1}}$=$\frac{1}{2}$($\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$),进而并项相加、放缩即得结论.
解答 (1)解:∵5(a1+a2)=a1+a2+a3+a4,
∴4(a1+a2)=a3+a4,
又∵数列{an}是各项均为正数的等比数列,
∴4(a1+a2)=q2(a1+a2),
解得:q=2或q=-2(舍),
∴数列{an}是首项为1、公比为2的等比数列,
∴an=2n-1,Sn=$\frac{1-{2}^{n}}{1-2}$=2n-1;
(2)证明:由(1)可知:$\frac{{a}_{n}}{{S}_{n}{S}_{n+1}}$=$\frac{{2}^{n-1}}{({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{1}{2}$($\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$),
∴Tn=$\frac{{a}_{1}}{{S}_{1}{S}_{2}}$+$\frac{{a}_{2}}{{S}_{2}{S}_{3}}$+…+$\frac{{a}_{n}}{{S}_{n}{S}_{n+1}}$
=$\frac{1}{2}$[($\frac{1}{2-1}$-$\frac{1}{{2}^{2}-1}$)+($\frac{1}{{2}^{2}-1}$-$\frac{1}{{2}^{3}-1}$)+…+($\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$)]
=$\frac{1}{2}$($\frac{1}{2-1}$-$\frac{1}{{2}^{n+1}-1}$)
<$\frac{1}{2}$.
点评 本题是一道关于数列与不等式的综合题,考查裂项相消法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
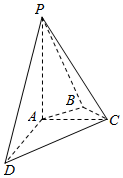 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表所示的统计表格.
设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表所示的统计表格.| i | 1 | 2 | 3 | 4 | 5 | 合计 |
| xi(百万元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
| wi(百万元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
| yi(百万元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com