
 设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表所示的统计表格.
设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表所示的统计表格.| i | 1 | 2 | 3 | 4 | 5 | 合计 |
| xi(百万元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
| wi(百万元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
| yi(百万元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
分析 (1)把所给的五组数据作为五个点的坐标描到直角坐标系中,得到散点图,
(2)根据散点图,y=c+dx3,适合销售额y关于明星代言费x的回归方程,
(3)①令ω=x3,则y=c+dω,是y关于ω的线性回归方程,根据最小二乘法做出线性回归方程的系数,写出线性回归方程,$\overline{y}$=1.15+1.21ω=1.15+1.21x3,构造辅助函数,利用函数的导数,求得函数的单调,根据函数的单调性求得纯收益z取最大值.
解答 解:(1)散点图如下: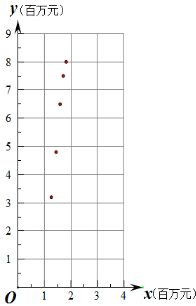
(2)根据散点图可知,y=c+dx3,适合销售额y关于明星代言费x的回归方程,
(3)①令ω=x3,则y=c+dω,是y关于ω的线性回归方程,
所以$\stackrel{^}{d}$=$\frac{\sum_{i=1}^{5}{ω}_{i}{y}_{i}-5\overline{ω}\overline{y}}{\sum_{i=1}^{5}({ω}_{i}-\overline{ω})^{2}}$≈1.21,$\stackrel{^}{c}$=$\overline{y}$-$\stackrel{^}{d}$•$\overline{ω}$≈1.15,
∴线性回归方程:$\overline{y}$=1.15+1.21ω=1.15+1.21x3,
z=f(x)=0.2y-0.726x,
=0.2(1.15+1.21x3)-0.726x,
=0.242x3-0.726x+0.23,其中x∈[1.00,2.00],
②令z′=0.726x2-0.726≥0,x≥1.00,
故z=f(x)在区间[1.00,2.00]内单调递增,
所以估计当明星的代言费为x=2.00百万时,纯收益z取最大值.
点评 本题考查线性回归方程的求法和应用,本题解题的关键是利用最小二乘法求出线性回归方程的系数,属于中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.
某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
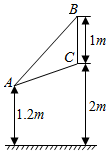 如图,化工厂的主控制表盘高BC=1米,表盘底边距地面2米,设值班人员坐在椅子上时,眼睛距地面1.2米,问值班人员坐在什么位置上看表盘效果最佳?(即视角∠BAC最大)
如图,化工厂的主控制表盘高BC=1米,表盘底边距地面2米,设值班人员坐在椅子上时,眼睛距地面1.2米,问值班人员坐在什么位置上看表盘效果最佳?(即视角∠BAC最大)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com