
分析 (Ⅰ)由f(x)为R上的奇函数,可得f(0)=0,解得m=2,再由奇函数的定义即可判断;
(Ⅱ)问题转化为m>$\frac{4}{{3}^{x}+1}$-2,根据函数的单调性求出m的范围即可.
解答 解:(Ⅰ)若f(x)为奇函数,即有f(0)=0,即m-$\frac{4}{{3}^{0}+1}$=0,解得m=2,
经检验f(-x)=-f(x),m=2符合题意;
(Ⅱ)由(Ⅰ)得:f(x)=2-$\frac{4}{{3}^{x}+1}$,
若不等式f(x)+m>0对一切x∈R恒成立,
即m>$\frac{4}{{3}^{x}+1}$-2,
当x→-∞时,$\frac{4}{{3}^{x}+1}$-2→2,
故m≥2.
点评 本题考查函数的奇偶性和单调性的判断和运用,考查不等式成立问题的解法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 微信控 | 非微信控 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
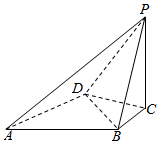 如图,在四棱锥P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.
如图,在四棱锥P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温(℃) | 32 | 34 | 38 | 40 |
| 销售额(元) | 421 | 446 | 497 | 520 |
| A. | 400元 | B. | 420元 | C. | 448元 | D. | 459元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.
某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com