
| 气温(℃) | 32 | 34 | 38 | 40 |
| 销售额(元) | 421 | 446 | 497 | 520 |
| A. | 400元 | B. | 420元 | C. | 448元 | D. | 459元 |
分析 求出数据样本中心点($\overline{x}$,$\overline{y}$),代入回归方程得出a,再利用回归方程进行数值估计.
解答 解:由$\overline{x}$=$\frac{32+34+38+40}{4}$=36,$\overline{y}$=$\frac{421+420+448+459}{4}$=471,
由线性回归方程$\stackrel{∧}{y}$=12x+$\stackrel{∧}{a}$,过样本中心点($\overline{x}$,$\overline{y}$),
∴$\stackrel{∧}{a}$=$\overline{y}$-12$\overline{x}$=39,
故线性回归方程为:$\stackrel{∧}{y}$=12x+5,
∴当x=35时,y=459,
故答案选:D.
点评 本题考查线性回归方程,考查最小二乘法的应用,考查利用线性回归方程求预测变量,属于基础题.


科目:高中数学 来源: 题型:解答题
| 患高血压 | 不患高血压 | 合计 | |
| 男 | m | 6 | |
| 女 | 12 | n | |
| 合计 | 60 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 使用4G | 未使用4G | 总计 | |
| 男用户 | 40 | 20 | 60 |
| 女用户 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P( K2≥k0) | 0.500 | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 0,455 | 2,706 | 3.841 | 6.635 | 10.828 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,0] | C. | [0,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
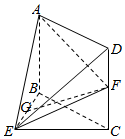 如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.
如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=2,G是线段BE的中点,点F在线段CD上且GF∥平面ADE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com