
分析 (1)根据函数f(x)的解析式,分母不为0,列出不等式求出解集即可;
(2)利用单调性的定义即可证明函数f(x)在[1,+∞)上是增函数.
解答 解:(1)∵函数f(x)=$\frac{2x-1}{x+1}$=2-$\frac{3}{x+1}$,
∴x+1≠0,解得x≠-1;
∴f(x)的定义域为{x|x≠-1};
(2)证明:任取x1,x2∈[1,+∞),且x1<x2,
∴f(x1)-f(x2)=(2-$\frac{3}{{x}_{1}+1}$)-(2-$\frac{3}{{x}_{2}+1}$)=$\frac{3}{{x}_{2}+1}$-$\frac{3}{{x}_{1}+1}$=$\frac{3{(x}_{1}{-x}_{2})}{{(x}_{1}+1){(x}_{2}+1)}$;
又1≤x1<x2,
∴3(x1-x2)<0,(x1+1)(x2+1)>0;
∴f(x1)-f(x2)<0,
即f(x1)<f(x2);
∴函数f(x)在[1,+∞)上是增函数.
点评 本题考查了求函数的定义域和利用定义证明函数的单调性问题,是基础题目.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 男生 | 15 | 35 | 50 |
| 女生 | 30 | 40 | 70 |
| 总计 | 45 | 75 | 120 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
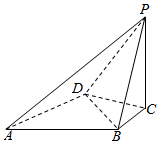 如图,在四棱锥P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.
如图,在四棱锥P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温(℃) | 32 | 34 | 38 | 40 |
| 销售额(元) | 421 | 446 | 497 | 520 |
| A. | 400元 | B. | 420元 | C. | 448元 | D. | 459元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.
某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线AB是以点E的圆心的圆的一部分,其中E(0,t)(0<t≤25),GF是圆的切线,且GF⊥AD,曲线BC是抛物线y=-ax2+50(a>0)的一部分,CD⊥AD,且CD恰好等于圆E的半径.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A真包含于B | B. | A=B | C. | A⊆B | D. | 无法比较 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{4}$或$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com