
分析 (1)先求出函数的导数,分类讨论a的范围,确定函数的单调性,从而求得函数的极值.
(2)取a=1,由(1)知 f(x)=lnx-$\frac{x-1}{x}$≥0,即 $\frac{1}{x}$≥1-lnx=ln$\frac{e}{x}$,取x=1,2,3…,n,累加可得要征的结论.
解答 解:(1)由题意可得 f′(x)=$\frac{x-a}{{x}^{2}}$,
∴当a>0时,令f′(x)=0,求得x=a,
由ax>0,求得x>0,函数的定义域为(0,+∞),
此时函数在(0,a)上,f′(x)<0,f(x)是减函数;在(a,+∞)上,f′(x)>0,f(x)是增函数,
故函数f(x)的极小值为f(a)=lna2,无最大值.
当a<0时,由ax>0,求得x<0,可得函数f(x)的定义域为(-∞,0),
此时函数(-∞,a)上,f′(x)=$\frac{x-a}{{x}^{2}}$<0,f(x)是减函数;在(a,0)上,f′(x)>0,f(x)是增函数,
故函数f(x)的极小值为f(a)=lna2,无最大值.
(2)证明:取a=1,由(1)知 f(x)=lnx-$\frac{x-1}{x}$≥f(1)=0,∴$\frac{1}{x}$≥1-lnx=ln$\frac{e}{x}$,
取x=1,2,3…,n,则 1+$\frac{1}{2}$+$\frac{1}{3}$…+$\frac{1}{n}$≥ln$\frac{e}{1}$+ln$\frac{e}{2}$+ln$\frac{e}{3}$+…+ln$\frac{e}{n}$=ln$\frac{{e}^{n}}{n!}$,
故要征得不等式1+$\frac{1}{2}$+$\frac{1}{3}$…+$\frac{1}{n}$≥ln$\frac{{e}^{n}}{n!}$ 成立.
点评 本题主要考查利用导数研究函数的单调性,求函数的极值,属于难题.


科目:高中数学 来源: 题型:解答题
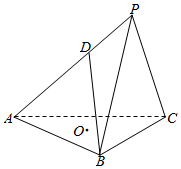 三棱锥P-ABC,底面ABC为边长为2$\sqrt{3}$的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为AP上一点,AD=2DP,O为底面三角形中心.
三棱锥P-ABC,底面ABC为边长为2$\sqrt{3}$的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为AP上一点,AD=2DP,O为底面三角形中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 微信控 | 非微信控 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com