
【题目】已知![]()
(1)求![]() 的轨迹
的轨迹![]()
(2)过轨迹![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() ,设直线
,设直线![]() 的斜率分别是
的斜率分别是![]() ,试问在三个斜率都存在且不为0的条件下,
,试问在三个斜率都存在且不为0的条件下, 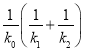 是否是定值,请说明理由,并加以证明.
是否是定值,请说明理由,并加以证明.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的短轴长为
)的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的标准方程;
(2)设M,N分别为椭圆C的左、右顶点,过点![]() 且不与x轴重合的直线
且不与x轴重合的直线![]() 与椭圆C相交于A,B两点是否存在实数t(
与椭圆C相交于A,B两点是否存在实数t(![]() ),使得直线
),使得直线![]() :
:![]() 与直线
与直线![]() 的交点P满足P,A,M三点共线?若存在,求出
的交点P满足P,A,M三点共线?若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子设备工厂生产一种电子元件,质量控制工程师要在产品出厂前将次品检出.估计这个厂生产的电子元件的次品率为0.2%,且电子元件是否为次品相互独立,一般的检测流程是:先把![]() 个
个![]() 电子元件串联起来成组进行检验,若检测通过,则全部为正品;若检测不通过,则至少有一个次品,再逐一检测,直到把所有的次品找出,若检验一个电子元件的花费为5分钱,检验一组(
电子元件串联起来成组进行检验,若检测通过,则全部为正品;若检测不通过,则至少有一个次品,再逐一检测,直到把所有的次品找出,若检验一个电子元件的花费为5分钱,检验一组(![]() 个)电子元件的花费为
个)电子元件的花费为![]() 分钱.
分钱.
(1)当![]() 时,估算一组待检元件中有次品的概率;
时,估算一组待检元件中有次品的概率;
(2)设每个电子元件检测费用的期望为![]() ,求
,求![]() 的表达式;
的表达式;
(3)试估计![]() 的值,使每个电子元件的检测费用的期望最小.(提示:用
的值,使每个电子元件的检测费用的期望最小.(提示:用![]() 进行估算)
进行估算)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体![]() 的棱长满足
的棱长满足![]() ,
,![]() ,现将四面体
,现将四面体![]() 放入一个主视图为等边三角形的圆锥中,使得四面体
放入一个主视图为等边三角形的圆锥中,使得四面体![]() 可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com