练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
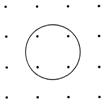
    2．如图所示，在排成4×4方阵的16个点中，中心位置4个点在某圆内，其余12个点在圆外．从16个点中任选3点，作为三角形的顶点，其中至少有一个顶点在圆内的三角形共有312个．

    分析 根据题意，按圆内取出的点的数目分3种情况讨论：①、取出的3个点都在圆内，②、在圆内取2点，圆外12点中取1点，③、在圆内取1点，圆外12点中取2点，分别求出每一种情况的取法数目，由分类计数原理计算可得答案．

    解答 解：根据题意，分3种情况讨论：
    ①、取出的3个点都在圆内，有C43=4种取法，即有4种取法，
    ②、在圆内取2点，圆外12点中取1点，有C42C101=60种，即有60种取法，
    ③、在圆内取1点，圆外12点中取2点，有C41（C122-4）=248种，即有248种取法，
    则至少有一个顶点在圆内的三角形有4+60+248=312个，
    故答案为：312．

    点评 本题考查排列、组合的实际应用，注意要分类讨论，要做到不重不漏．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．观察下列各式：1=12，2+3+4=32，3+4+5+6=52，4+5+6+7+8+9+10=72，…，可以得出的一般结论是（　　）
    A．n+（n+1）+（n+2）+…+（3n-2）=n2B．n+（n+1）+（n+2）+…+（3n-2）=（2n-1）2
    C．n+（n+1）+（n+2）+…+（3n-1）=n2D．n+（n+1）+（n+2）+…+（3n-1）=（2n-1）2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知函数f（x）=4x3+ax2+bx+5在x=-1与x=$\frac{3}{2}$处有极值，则函数的单调递减区间为（-1，$\frac{3}{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知数列{an}中，a3=2，a7=1，若数列$\left\{{\frac{1}{{1+{a_n}}}}\right\}$是等差数列，则a11等于（　　）
    A．0B．$\frac{1}{3}$C．$\frac{1}{6}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知实数x，y满足-1≤x+y≤4且2≤x-y≤3，则不等式围成的区域面积为$\frac{5}{2}$，则2x-3y的取值范围是[3，8]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知向量$\vec a=（1，2）$，$\vec b=（1，0）$，$\vec c=（3，4）$．若λ为实数，$（\overrightarrow a+λ\overrightarrow b）∥\overrightarrow c$，则λ=（　　）
    A．2B．1C．$\frac{1}{2}$D．$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数f（x）=（x2-a+1）ex，g（x）=（x2-2）ex+2
    （1）若函数f（x）在区间[-2，2]上是单调函数，求实数a的取值范围；
    （2）若f（x）有两个不同的极值点m，n（m＜n），且2（m+n）≤mn-1，记F（x）=e2f（x）+g（x），求F（m）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知x+y+z=1．
    证明：（1）x2+y2+z2≥xy+yz+zx，
    （2）x2+y2+z2≥$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．2cos275°-1的值为（　　）
    A．$\frac{{\sqrt{3}}}{2}$B．-$\frac{{\sqrt{3}}}{2}$C．-$\frac{1}{2}$D．$\frac{1}{2}$

    查看答案和解析>>

    同步练习册答案