
分析 (1)利用已知条件,平方,通过重要不等式,转化证明即可.
(2)利用平方化简,结合(1)即可推出结果.
解答 (本题满分12分)
证明:(1)∵x+y+z=1,∴(x+y+z)2=x2+y2+z2+2(xy+yz+zx)=1
又∵x2+y2≥2xy,y2+z2≥2yz,z2+x2≥2xz,
∴2(x2+y2+z2)≥2(xy+yz+zx),
即x2+y2+z2≥xy+yz+zx,
(2)∵x+y+z=1,∴(x+y+z)2=x2+y2+z2+2(xy+yz+zx)=1
∴1=x2+y2+z2+2(xy+yz+zx)≤3(x2+y2+z2).
∴x2+y2+z2≥$\frac{1}{3}$.
点评 本题考查不等式的证明,综合法的应用,考查逻辑推理能力.


科目:高中数学 来源: 题型:选择题
| A. | 1+3i | B. | 1-3i | C. | 3-i | D. | 3+i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
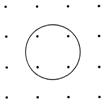 如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.
如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
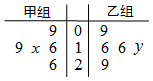 如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )| A. | 7、8 | B. | 5、7 | C. | 8、5 | D. | 7、7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,1) | C. | (-∞,-1) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com