Question

【题目】甲、乙两人要对C处进行考察，甲在A处，乙在B处，基地在O处，此时∠AOB＝90°，测得|AC|＝5 km，|BC|＝km，|AO|＝|BO|＝2 km，如图所示，试问甲、乙两人应以什么方向走，才能使两人的行程之和最小？

Answer 1

【答案】甲应以与OB平行的方向行走，乙应沿斜率为的直线向上方行走，才能使他们的行程和最小

【解析】试题分析：以O为原点，OB为x轴，建立直角坐标系，由两点间线段最短，所以甲沿着直线AC，乙沿着直线BC行走即可，只需求出C点坐标即可得直线的斜率，即为行走方向.

试题解析：

以O为原点，OB为x轴，建立直角坐标系(如图所示)，

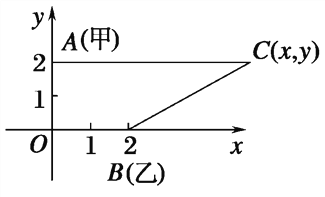
设C(x，y)，则有A(0,2)，B(2,0)，

由|AC|＝5，有＝5，①

|BC|＝，有＝.②

由①②解得或

由x、y的实际意义知x>0，y>0，∴C(5,2)．

而A(0,2)，∴AC∥x轴，即AC∥OB.

由B(2,0)、C(5,2)，知kBC＝＝.

故甲应以与OB平行的方向行走，乙应沿斜率为的直线向上方行走，才能使他们的行程和最小