
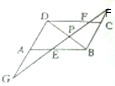
 如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.
如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.分析 (1)利用AB∥CD,可得$\frac{PE}{PF}$=$\frac{PB}{PD}$,AD∥BC,可得$\frac{PH}{PG}$=$\frac{PB}{PD}$,从而$\frac{PE}{PF}$=$\frac{PH}{PG}$,即可证明结论;
(2)利用AB∥CD,可得$\frac{PE}{PC}$=$\frac{PB}{PD}$,AD∥BC,可得$\frac{PC}{PG}$=$\frac{PB}{PD}$,从而$\frac{PE}{PC}$=$\frac{PC}{PG}$,即可得出结论.
解答 (1)证明:∵AB∥CD,∴$\frac{PE}{PF}$=$\frac{PB}{PD}$,
∵AD∥BC,∴$\frac{PH}{PG}$=$\frac{PB}{PD}$,
∴$\frac{PE}{PF}$=$\frac{PH}{PG}$.
∴PE•PG=PH•PF.(6分)
(2)解:由题意可得到图形,关系式为PC2=PE•PG,
∵AB∥CD,∴$\frac{PE}{PC}$=$\frac{PB}{PD}$,
∵AD∥BC,∴$\frac{PC}{PG}$=$\frac{PB}{PD}$,
∴$\frac{PE}{PC}$=$\frac{PC}{PG}$,即PC2=PE•PG.(12分)
点评 本题考查平行线分线段成比例的性质,考查学生分析解决问题的能力,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 6m | B. | 8m | C. | 10m | D. | 12m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成下面的茎叶图若两种品牌销量的平均数为$\overline{{x}_{甲}}$与$\overline{{x}_{乙}}$,方差为s${\;}_{甲}^{2}$与s${\;}_{乙}^{2}$,则( )
某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成下面的茎叶图若两种品牌销量的平均数为$\overline{{x}_{甲}}$与$\overline{{x}_{乙}}$,方差为s${\;}_{甲}^{2}$与s${\;}_{乙}^{2}$,则( )| A. | $\overline{{x}_{甲}}$$<\overline{{x}_{乙}}$,s${\;}_{甲}^{2}$$<{s}_{乙}^{2}$ | B. | $\overline{{x}_{甲}}$$>\overrightarrow{{x}_{乙}}$,s${\;}_{甲}^{2}$$<{s}_{乙}^{2}$ | ||
| C. | $\overline{{x}_{甲}}$$>\overrightarrow{{x}_{乙}}$,s${\;}_{甲}^{2}$>s${\;}_{乙}^{2}$ | D. | $\overline{{x}_{甲}}$$<\overline{{x}_{乙}}$,s${\;}_{甲}^{2}$$>{s}_{乙}^{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的几何体中,四边形ABCD为平行四边形,∠ACD=90°,AB=1,AD=2,ABEF为正方形,平面ABEF⊥平面ABCD,P为DF的中点.AN⊥CF,垂足为N.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACD=90°,AB=1,AD=2,ABEF为正方形,平面ABEF⊥平面ABCD,P为DF的中点.AN⊥CF,垂足为N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com