
分析 (1)在数列递推式中,取n=2,结合已知a2=12求得数列首项;
(2)在数列递推式中,取n=-1得另一递推式,作差后可得数列{an}为等差数列,由等差数列的通项公式得答案;
(3)求出等差数列的前n项和,取倒数后利用裂项相消法求出$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$得答案.
解答 (1)解:由Sn=nan-3n(n-1),得a1+a2=2a2-3×2×(2-1),
即a1=a2-6,
∵a2=12,∴a1=12-6=6;
(2)解:由Sn=nan-3n(n-1),得
Sn-1=(n-1)an-1-3(n-1)(n-2)(n≥2),
两式作差得:an=nan-(n-1)an-1-6n+6,即an-an-1=6(n≥2).
∴数列{an}是以6为首项,以6为公差的等差数列,
∴an=6+6(n-1)=6n;
(3)证明:${S}_{n}=6n+\frac{6n(n-1)}{2}=3n(n+1)$,
则$\frac{1}{{S}_{n}}=\frac{1}{3n(n+1)}=\frac{1}{3}(\frac{1}{n}-\frac{1}{n+1})$,
∴$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$=$\frac{1}{3}(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1})$=$\frac{1}{3}(1-\frac{1}{n+1})<\frac{1}{3}$.
点评 本题考查了数列递推式,考查了等差关系的确定,训练了裂项相消法求数列的和,是中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)(A>0且ω>0,0<φ<$\frac{π}{2}$)的部分图象,如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0且ω>0,0<φ<$\frac{π}{2}$)的部分图象,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
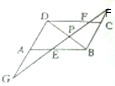 如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.
如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 重庆巴蜀中学高三的某位学生的10次数学考试成绩的茎叶图如图所示,则该生数学成绩在(135,140)内的概率为( )
重庆巴蜀中学高三的某位学生的10次数学考试成绩的茎叶图如图所示,则该生数学成绩在(135,140)内的概率为( )| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com