
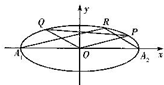
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,P,Q,T为椭圆异于A1,A2的点,若椭圆C的焦距为2$\sqrt{2}$,且椭圆过点M($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{7}}{2}$).
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1,A2,P,Q,T为椭圆异于A1,A2的点,若椭圆C的焦距为2$\sqrt{2}$,且椭圆过点M($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{7}}{2}$).分析 (1)由题意可知c=$\sqrt{2}$,求得焦点坐标,由两点之间的距离公式求得丨MF1丨=$\frac{5}{2}$,丨MF2丨=$\frac{3}{2}$,根据椭圆的定义可知丨MF1丨+丨MF2丨=2a及b2=a2-c2,即可求得a和b的值,求得椭圆方程;
(2)将直线A1R的方程代入椭圆方程,求得R点坐标,由斜率公式即可求得${k}_{{A}_{2}k}$,由题意可知,由证明证OQ∥A2R,只需证${k}_{{A}_{2}k}$=kOP,因此只需证明kOR•kOP=-$\frac{1}{2}$,当直线PQ的斜率不存在,根据三角形的面积公式,求得x1•x2=2,y1•y2=-1,由kOR•kOP=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,当斜率存在时,设直线PQ的方程,代入椭圆方程,由韦达定理,弦长公式及三角形的面积公式求得m2=2k2+1,kOR•kOP=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=$\frac{{k}^{2}{x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}}{{{x}_{1}x}_{2}}$=-$\frac{1}{2}$,因此OQ∥A2R.
解答 解:(1)由题意可知:2c=2$\sqrt{2}$,即c=$\sqrt{2}$,则椭圆的焦点坐标F1(-$\sqrt{2}$,0),F2($\sqrt{2}$,0),
则丨MF1丨=$\frac{5}{2}$,丨MF2丨=$\frac{3}{2}$,
由椭圆的定义可知:丨MF1丨+丨MF2丨=2a,解得:a=2,
由b2=a2-c2=4-2=2,
∴椭圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;
(2)证明:设直线A1R的方程为y=kOP(x+2),代入椭圆方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,
整理得:(2${k}_{OP}^{2}$+1)x2+8${k}_{OP}^{2}$x+8${k}_{OP}^{2}$-4=0,
由一元二次方程的两个根-2和xB,
可知:xR=$\frac{2-4{k}_{OP}^{2}}{2{k}_{OP}^{2}+1}$,yR=$\frac{4{k}_{OP}}{2{k}_{OP}^{2}+1}$,从而${k}_{{A}_{2}k}$=$\frac{\frac{4{k}_{OP}}{2{k}_{OP}^{2}+1}}{\frac{2-4{k}_{OP}^{2}}{2{k}_{OP}^{2}+1}-2}$=-$\frac{1}{2{k}_{OP}}$,
要证OQ∥A2R,只需证${k}_{{A}_{2}k}$=kOP,
即证-$\frac{1}{2{k}_{OP}}$=kOP,即kOR•kOP=-$\frac{1}{2}$,
设P(x1,y1),Q(x2,y2),
若直线PQ的斜率不存在,由S△OPQ=$\sqrt{2}$,可知:x1•x2=2,y1•y2=-1,
∴kOR•kOP=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,
当直线PQ的斜率存在,设PQ的方程为y=kx+m,代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,
整理得:(2k2+1)x2+4kmx+2m2-4=0,
由△=8(4k2+2-m2)>0,
由韦达定理可知:x1+x2=-$\frac{4km}{2{k}^{2}+1}$,x1•x2=$\frac{2{m}^{2}-4}{2{k}^{2}+1}$,
由S△OPQ=$\frac{1}{2}$丨m丨•丨x1-x2丨=$\frac{1}{2}$丨m丨•$\frac{\sqrt{8(4{k}^{2}+2-{m}^{2})}}{2{k}^{2}+1}$=$\sqrt{2}$,
整理得:m4-(4k2+2)m2+(2k2+1)2=0,得m2=2k2+1,满足△>0,
kOR•kOP=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=$\frac{{k}^{2}{x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}}{{{x}_{1}x}_{2}}$=$\frac{{m}^{2}-4{k}^{2}}{2{m}^{2}-4}$=$\frac{2{k}^{2}+1-4{k}^{2}}{2(2{k}^{2}+1)-4}$=-$\frac{1}{2}$,
综上可知:OQ∥A2R.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,韦达定理,弦长公式及三角形的面积公式的综合运用,考查分析法在证明题的应用,考查分类讨论思想,属于中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com