Question

7．O是△ABC的外接圆的圆心，若AC=3，$\overrightarrow{AO}$•$\overrightarrow{BC}$=2，则AB=$\sqrt{5}$．

Answer 1

分析 把$\overrightarrow{BC}$=$\overrightarrow{AC}-\overrightarrow{AB}$代入$\overrightarrow{AO}$•$\overrightarrow{BC}$=2，再转化为$|\overrightarrow{AB}|$与$|\overrightarrow{AC}|$的等式求解．

解答 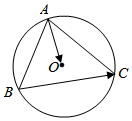解：如图
$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\overrightarrow{AO}•（\overrightarrow{AC}-\overrightarrow{AB}）=\frac{1}{2}|\overrightarrow{AC}{|}^{2}-\frac{1}{2}|\overrightarrow{AB}{|}^{2}=2$，
∵AC=3，
∴$\frac{1}{2}|\overrightarrow{AB}{|}^{2}=\frac{1}{2}×{3}^{2}-2=\frac{5}{2}$，则$|\overrightarrow{AB}|=\sqrt{5}$，
∴AB=$\sqrt{5}$．
故答案为：$\sqrt{5}$．

点评 本题考查平面向量的数量积运算，考查了向量在向量方向上投影的概念，体现了数学转化思想方法，是中档题．