
| A. | a+c-b | B. | a+2b-c | C. | b+c-a | D. | a+c-2b |
分析 $\overrightarrow{OD}$与$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$之间难以建立直接的关系,挖掘隐含条件$\overrightarrow{AD}$=$\overrightarrow{BC}$,寻找$\overrightarrow{OD}$、$\overrightarrow{a}$与$\overrightarrow{AD}$以及$\overrightarrow{b}$、$\overrightarrow{c}$与$\overrightarrow{BC}$的关系可间接获解.
解答 解:∵在四棱锥O-ABCD中,底面ABCD是平行四边形,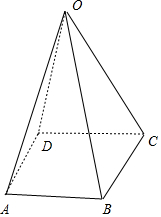
∴$\overrightarrow{AO}+\overrightarrow{OD}$=$\overrightarrow{AD}$,
$\overrightarrow{BO}+\overrightarrow{OC}$=$\overrightarrow{BC}=\overrightarrow{AD}$,
∴$\overrightarrow{AO}+\overrightarrow{OD}$=$\overrightarrow{BO}+\overrightarrow{OC}$,
∴$\overrightarrow{OD}$=-$\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{OC}$
=$\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}$
=$\overrightarrow{a}+\overrightarrow{c}-\overrightarrow{b}$.
故选:A.
点评 本题考查向量的求法,是基础题,解题时要认真审题,注意空间向量加法法则的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
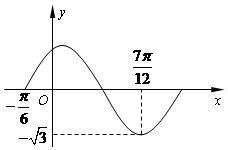 设函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,且A>0,ω>0,0<φ<π)的部分图象如图所示.
设函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,且A>0,ω>0,0<φ<π)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
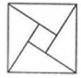 2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么sin2θ的值为( )
2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么sin2θ的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{23}{24}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{e},e})$ | B. | $({\frac{1}{2e},\frac{1}{e}})$ | C. | $({-∞,\frac{1}{2e}})$ | D. | $({\frac{1}{2e},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-3且x≠-2} | B. | {x|x≥-3且x≠2} | C. | {x|x≥-3} | D. | {x|x≥-2且x≠3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com