
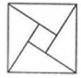
 2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么sin2θ的值为( )
2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么sin2θ的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{23}{24}$ | D. | $\frac{24}{25}$ |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区.
如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+c-b | B. | a+2b-c | C. | b+c-a | D. | a+c-2b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com