Question

在三棱柱ABC-A₁B₁C₁中，已知AA₁=8，AC=AB=5，BC=6，点A₁在底面ABC的投影是线段BC的中点O，在侧棱AA₁上存在一点E，且OE⊥B₁C．
（1）证明：OE⊥面BB₁C₁C．
（2）求出AE的长；
（3）求二面角A₁-B₁C-C₁的大小．

Answer 1

考点：与二面角有关的立体几何综合题,直线与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（1）利用线面垂直的判定定理；（2）证明Rt△A₁OA，OE⊥AA₁，由射影定理可求；（3）向量法解决．

解答： （1）证明：∵点A₁在底面ABC的投影是线段BC的中点O，
∴A₁O⊥面ABC，BC?面ABC，∴A₁O⊥BC，
又∵AC=AB=5，线段BC的中点O，
∴BC⊥AO，A₁O∩AO=O，
∴BC⊥面A₁OA，EO?面A₁OA，EO⊥BC，又∵OE⊥B₁C，B₁C∩BC=C，B₁C?面BB₁C₁C，BC?面BB₁C₁C
，∴OE⊥面BB₁C₁C；
（2）解：∵AA₁=8，AC=AB=5，BC=6，线段BC的中点O，
∴AO⊥BC，∴AO=4，由（1）知A₁O⊥面ABC，AO?面ABC，
∴A₁O⊥AO，
Rt△A₁OA，由（1）知，OE⊥面BB₁C₁C．BB₁?面BB₁C₁C，
∴OE⊥BB₁，∵三棱柱ABC-A₁B₁C₁，AA₁∥BB₁，
∴OE⊥AA₁，∴OA²=AE•AA₁，∴AE=2；
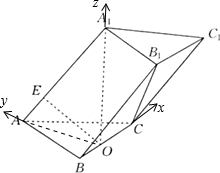
（3）分别以OC、OA、OA₁为x、y、z轴建立空间坐标系，C（3，0，0），A₁（0，0，4

3

），A（0，4，0），B（-3，0，0），
∵

AB

=

A1B1

，∴B₁（-3，-4，4

3

），
∵

AA1

=

CC1

，∴C₁（3，-4，4

3

），

CA1

=（-3，0，4

3

），

CB1

=（-6，-4，4

3

），

CC1

=（0，-4，4

3

），
设面A₁B₁C的法向量

m

=（x，y，z），

m • CA1 =0 m • CB1 =0

，取

m

=（1，-

3

4

，

3

4

），设面，C₁B₁C的法向量

n

=（x，y，z），

n • CB1 =0 n • CC1 =0

，取

n

=（0，

3

，1），
cos＜

m

，

n

＞=

m • n

| m || n |

=-

21

14

，由图知，二面角A₁-B₁C-C₁的大小为arccos

21

14

点评：本题考查空间直线和平面位置关系的确定；线段的长度；还考查了二面角大小求解，本题具有建立空间直角坐标系的良好空间特征，故用向量法为宜．