
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,过点
的焦点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,抛物线
,抛物线![]() 在
在![]() 两点处的切线分别是
两点处的切线分别是![]() ,且
,且![]() 相交于点
相交于点![]() ,则
,则![]() 的小值是___.
的小值是___.
【答案】6
【解析】
设直线l的方程为:y=kx+1,A(![]() ),B(
),B(![]() ).联立化为:x2﹣4kx﹣4=0,利用根与系数的关系可得|AB|=
).联立化为:x2﹣4kx﹣4=0,利用根与系数的关系可得|AB|=![]() =k(
=k(![]() )+4.对x2=4y两边求导可得:y′
)+4.对x2=4y两边求导可得:y′![]() ,可得切线PA的方程为:y﹣
,可得切线PA的方程为:y﹣![]() (x﹣
(x﹣![]() ),切线PB的方程为:y﹣
),切线PB的方程为:y﹣![]() (x﹣
(x﹣![]() ),联立解得P点坐标,可得代入|PF|
),联立解得P点坐标,可得代入|PF|![]() ,利用导数研究函数的单调性极值即可得出.
,利用导数研究函数的单调性极值即可得出.
设直线l的方程为:y=kx+1,A(![]() ),B(
),B(![]() .
.
联立![]() ,化为:x2﹣4kx﹣4=0,
,化为:x2﹣4kx﹣4=0,
可得:![]() =4k,
=4k,![]() =﹣4,
=﹣4,
|AB|=![]() =k(
=k(![]() )+4=4k2+4.
)+4=4k2+4.
对x2=4y两边求导可得:y′![]() ,
,
可得切线PA的方程为:y﹣![]() (x﹣
(x﹣![]() )
)
切线PB的方程为:y﹣![]() (x﹣
(x﹣![]() ),
),
联立解得:x![]() (
(![]() )=2k,y
)=2k,y![]() =﹣1.∴P(2k,﹣1).
=﹣1.∴P(2k,﹣1).
∴|PF|![]() .
.
∴|PF|![]() ,
,
令![]() t≥2.
t≥2.
则|PF|![]() t
t![]() f(t),
f(t),
f′(t)=1![]() ,当t>4, f′(t)>0;
,当t>4, f′(t)>0;![]() t<4, f′(t)<0
t<4, f′(t)<0
可得t=4时,函数f(t)取得极小值即最小值f(4)=6.当且仅当k![]() 时取等号.
时取等号.
故答案为:6.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了检验设备M与设备N的生产效率,研究人员作出统计,得到如下表所示的结果,则
设备M | 设备N | |
生产出的合格产品 | 48 | 43 |
生产出的不合格产品 | 2 | 7 |
附:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]() .
.
A. 有90%的把握认为生产的产品质量与设备的选择有关
B. 没有90%的把握认为生产的产品质量与设备的选择有关
C. 可以在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择有关
D. 不能在犯错误的概率不超过0.1的前提下认为生产的产品质量与设备的选择有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两条异面直线,直线
是两条异面直线,直线![]() 与
与![]() 都垂直,则下列说法正确的是( )
都垂直,则下列说法正确的是( )
A. 若![]() 平面
平面![]() ,则
,则![]()
B. 若![]() 平面
平面![]() ,则
,则![]() ,
,![]()
C. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
D. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x(万辆) | 100 | 102 | 108 | 114 | 116 |
PM2.5的浓度y(微克/立方米) | 78 | 80 | 84 | 88 | 90 |
(1)根据上表数据,用最小二乘法,求出y关于x的线性回归方程![]() x
x![]() ;
;
(2)若周六同一时间段车流量200万辆,试根据(1)求出的线性回归方程,预测此时PM2.5的浓度为多少?
(参考公式: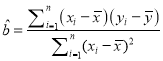 ,
,![]()
![]() ;参考数据:
;参考数据:![]() xi=540,
xi=540,![]() yi=420)
yi=420)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六棱锥![]() 中,底面
中,底面![]() 是正六边形,
是正六边形,![]() 底面
底面![]() ,给出下列四个命题:
,给出下列四个命题:
①线段![]() 的长是点
的长是点![]() 到线段
到线段![]() 的距离;
的距离;
②异面直线![]() 与
与![]() 所成角是
所成角是![]() ;
;
③线段![]() 的长是直线
的长是直线![]() 与平面
与平面![]() 的距离;
的距离;
④![]() 是二面角
是二面角![]() 平面角.
平面角.
其中所有真命题的序号是_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.

(1)求证:图2中,平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,马路![]() 南边有一小池塘,池塘岸
南边有一小池塘,池塘岸![]() 长40米,池塘的最远端
长40米,池塘的最远端![]() 到
到![]() 的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路
的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路![]() ,且
,且![]() 均与小池塘岸线相切,记
均与小池塘岸线相切,记![]() .
.

(1)求小路的总长,用![]() 表示;
表示;
(2)若在小路与小池塘之间(图中阴影区域)铺上草坪,求所需铺草坪面积最小时,![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 距离之和的最小值为( )
距离之和的最小值为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com