
【题目】六棱锥![]() 中,底面
中,底面![]() 是正六边形,
是正六边形,![]() 底面
底面![]() ,给出下列四个命题:
,给出下列四个命题:
①线段![]() 的长是点
的长是点![]() 到线段
到线段![]() 的距离;
的距离;
②异面直线![]() 与
与![]() 所成角是
所成角是![]() ;
;
③线段![]() 的长是直线
的长是直线![]() 与平面
与平面![]() 的距离;
的距离;
④![]() 是二面角
是二面角![]() 平面角.
平面角.
其中所有真命题的序号是_______________.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】a,b为空间两条互相垂直的直线,等腰直角三角形![]() 的直角边
的直角边![]() 所在直线与a,b都垂直,斜边
所在直线与a,b都垂直,斜边![]() 以
以![]() 为旋转轴选择,有下列结论:
为旋转轴选择,有下列结论:
①当直线![]() 与a成60°角时,
与a成60°角时,![]() 与b成30°角;
与b成30°角;
②当直线![]() 与a成60°角时,
与a成60°角时,![]() 与b成60°角;
与b成60°角;
③直线![]() 与a所成角的最小值为45°;
与a所成角的最小值为45°;
④直线![]() 与a所成角的最大值为60°;
与a所成角的最大值为60°;
其中正确的是_______.(填写所以正确结论的编号).
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后,发布了《个人所得税专项附加扣除暂行办法》,明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用,并公布了相应的定额扣除标准,决定自2019年1月1日起施行,某机关为了调查内部职员对新个税方案的满意程度与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁及以下 | 40岁以上 | 合计 | |
基本满意 | 15 | 10 | 25 |
很满意 | 25 | 30 | 55 |
合计 | 40 | 40 | 80 |
(1)根据列联表,能否有85%的把握认为满意程度与年龄有关?
(2)若已经在满意程度为“基本满意”的职员中用分层抽样的方式选取了5名职员,现从这5名职员中随机选取3名进行面谈求面谈的职员中恰有2名年龄在40岁及以下的概率.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
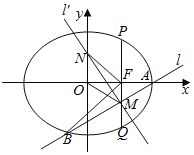
【题目】如图,已知椭圆C:![]() 1(a>b>0)的右焦点为F,A(2,0)是椭圆的右顶点,过F且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3.
1(a>b>0)的右焦点为F,A(2,0)是椭圆的右顶点,过F且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3.
(1)求椭圆的方程;
(2)过点A的直线l与椭圆交于另一点B,垂直于l的直线l′与直线l交于点M,与y轴交于点N,若FB⊥FN且|MO|=|MA|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.
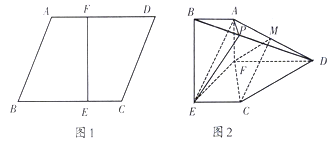
(1)求证:图2中,平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.
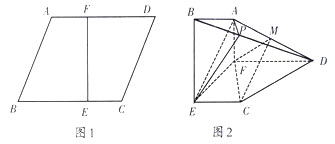
(1)若平面![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(2)是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
(Ⅰ)若点P在椭圆C的内部,求直线AM的斜率的取值范围;
(Ⅱ)设椭圆C的右焦点为F,点Q在y轴上,且AQ∥BM,求证:∠PFQ为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com