练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    若在其定义域上单调递减，求的取值范围；

    若存在两个不同极值点与，且，求证.

    【答案】（1）（2）见解析

    【解析】

    先对函数求导，由在其定义域上单调递减，得到恒成立，即恒成立，用导数的方法求出的最小值即可；

    （2）若存在两个不同极值点与，且，欲证：，只需证：，即证，再根据，得到，，再令，得到，设，由导数方法研究其单调性即可得出结论.

    解：（1）由于的定义域为，且，若在其定义域上单调递减，则恒成立，即恒成立.

    令，

    则随着的变化，与的变化如下表所示

    -

    0

    +

    ↘

    极小值

    ↗

    所以.

    所以

    （2）若存在两个不同极值点与，且，

    欲证：.

    只需证：.

    只需证：.

    只需证：.

    因为，，，，

    所以，

    所以

    令，则，则，

    设，则，

    可知函数在上单调递增

    所以 .

    所以成立.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某机构对A市居民手机内安装的“APP”(英文Application的缩写，一般指手机软件)的个数和用途进行调研，在使用智能手机的居民中随机抽取了100人，获得了他们手机内安装APP的个数，整理得到如图所示频率分布直方图：

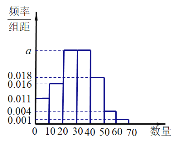
    （Ⅰ）从A市随机抽取一名使用智能手机的居民，试估计该居民手机内安装APP的个数不低于30的概率；

    （Ⅱ）从A市随机抽取3名使用智能手机的居民进一步做调研，用X表示这3人中手机内安装APP的个数在[20,40)的人数．

    ①求随机变量X的分布列及数学期望；

    ②用Y1表示这3人中安装APP个数低于20的人数，用Y2表示这3人中手机内安装APP的个数不低于40的人数．试比较EY1和EY2的大小．(只需写出结论)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】六棱锥中，底面是正六边形，底面，给出下列四个命题：

    ①线段的长是点到线段的距离；

    ②异面直线与所成角是；

    ③线段的长是直线与平面的距离；

    ④是二面角平面角.

    其中所有真命题的序号是_______________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，抛物线的焦点为F，过F的动直线l交于M、N两点.

    （1）若l垂直于x轴，且线段MN的长为1，求的方程；

    （2）若，求线段MN的中点P的轨迹方程；

    （3）求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，马路南边有一小池塘，池塘岸长40米，池塘的最远端到的距离为400米，且池塘的边界为抛物线型，现要在池塘的周边建一个等腰梯形的环池塘小路，且均与小池塘岸线相切，记.

    （1）求小路的总长，用表示；

    （2）若在小路与小池塘之间（图中阴影区域）铺上草坪，求所需铺草坪面积最小时，的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （Ⅰ）当时，求的图象在点处的切线方程；

    （Ⅱ）设函数，讨论函数的零点个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（t为参数），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，圆的极坐标方程为．

    （Ⅰ）求的普通方程和的直角坐标方程；

    （Ⅱ）过曲线上任一点作与夹角为45°的直线，交于点，求的最大值与最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的上下两个焦点分别为，过点与轴垂直的直线交椭圆于两点，的面积为，椭圆的长轴长是短轴长的倍.

    （1）求椭圆的标准方程；

    （2）已知为坐标原点，直线与轴交于点，与椭园交于两个不同的点，若存在实数，使得，求的取值范围，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆（常数），P是曲线C上的动点，M是曲线C的右顶点，定点A的坐标为.

    （1）若M与A重合，求曲线C的焦距.

    （2）若，求的最大值与最小值.

    查看答案和解析>>

    同步练习册答案