
【题目】已知椭圆![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 两点,
两点,![]() 的面积为
的面积为![]() ,椭圆
,椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭园
,与椭园![]() 交于
交于![]() 两个不同的点,若存在实数
两个不同的点,若存在实数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围,
的取值范围,
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 1(a>b>0)的右焦点为F,A(2,0)是椭圆的右顶点,过F且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3.
1(a>b>0)的右焦点为F,A(2,0)是椭圆的右顶点,过F且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3.
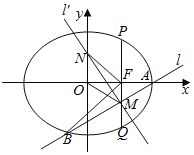
(1)求椭圆的方程;
(2)过点A的直线l与椭圆交于另一点B,垂直于l的直线l′与直线l交于点M,与y轴交于点N,若FB⊥FN且|MO|=|MA|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,O为AD中点,AB=1,AD=2,AC=CD=![]() .
.
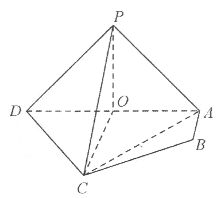
(1)证明:直线AB∥平面PCO;
(2)求二面角P-CD-A的余弦值;
(3)在棱PB上是否存在点N,使AN⊥平面PCD,若存在,求线段BN的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下图给出的2000年至2016年我国实际利用外资情况,以下结论正确的是

A. 2000年以来我国实际利用外资规模与年份负相关
B. 2010年以来我国实际利用外资规模逐年增加
C. 2008年我国实际利用外资同比增速最大
D. 2010年以来我国实际利用外资同比增速最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
(Ⅰ)若点P在椭圆C的内部,求直线AM的斜率的取值范围;
(Ⅱ)设椭圆C的右焦点为F,点Q在y轴上,且AQ∥BM,求证:∠PFQ为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系中,直线
轴的正半轴为极轴建立极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求C的普通方程和直线![]() 的倾斜角;
的倾斜角;
(Ⅱ)设点![]() (0,2),
(0,2),![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取一天,若已知所选取该天的热奶茶销售杯数大于120,求所选取该天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .参考公式:
.参考公式: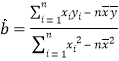 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com