
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数),以坐标原点
(t为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,圆
轴正半轴为极轴,建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)过曲线![]() 上任一点
上任一点![]() 作与
作与![]() 夹角为45°的直线,交
夹角为45°的直线,交![]() 于点
于点![]() ,求
,求![]() 的最大值与最小值.
的最大值与最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后,发布了《个人所得税专项附加扣除暂行办法》,明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用,并公布了相应的定额扣除标准,决定自2019年1月1日起施行,某机关为了调查内部职员对新个税方案的满意程度与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁及以下 | 40岁以上 | 合计 | |
基本满意 | 15 | 10 | 25 |
很满意 | 25 | 30 | 55 |
合计 | 40 | 40 | 80 |
(1)根据列联表,能否有85%的把握认为满意程度与年龄有关?
(2)若已经在满意程度为“基本满意”的职员中用分层抽样的方式选取了5名职员,现从这5名职员中随机选取3名进行面谈求面谈的职员中恰有2名年龄在40岁及以下的概率.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.
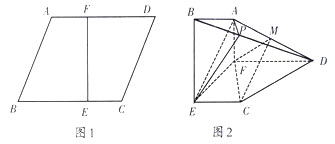
(1)若平面![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(2)是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A.一条直线与两个平行平面中的一个平行,则必与另一个平面平行
B.空间中两条直线要么平行,要么相交
C.空间中任意的三个点都能唯一确定一个平面
D.对于空间中任意两条直线,总存在平面与这两条直线都平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,O为AD中点,AB=1,AD=2,AC=CD=![]() .
.
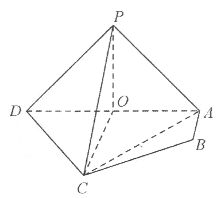
(1)证明:直线AB∥平面PCO;
(2)求二面角P-CD-A的余弦值;
(3)在棱PB上是否存在点N,使AN⊥平面PCD,若存在,求线段BN的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下图给出的2000年至2016年我国实际利用外资情况,以下结论正确的是

A. 2000年以来我国实际利用外资规模与年份负相关
B. 2010年以来我国实际利用外资规模逐年增加
C. 2008年我国实际利用外资同比增速最大
D. 2010年以来我国实际利用外资同比增速最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
(Ⅰ)若点P在椭圆C的内部,求直线AM的斜率的取值范围;
(Ⅱ)设椭圆C的右焦点为F,点Q在y轴上,且AQ∥BM,求证:∠PFQ为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:“方程:![]() 表示焦点在x轴上的双曲线”;命题q:“关于x的不等式x2+2ax+1≥0在R上恒成立”.
表示焦点在x轴上的双曲线”;命题q:“关于x的不等式x2+2ax+1≥0在R上恒成立”.
(1)若命题p为真命题,求实数a的取值范围;
(2)若命题“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com