
已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品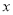 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为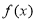 万元,且
万元,且
(1)写出年利润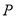 (万元)关于年产品
(万元)关于年产品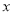 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该企业生产此产品所获年利润最大?
(注:年利润=年销售收入-年总成本)
(1) (2)9
(2)9
【解析】
试题分析:利用基本不等式解决实际问题时,应先仔细阅读题目信息,理解题意,明确其中的数量关系,并引入变量,依题意列出相应的函数关系式,然后利用基本不等式求解;(2)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(3)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.
试题解析:(1)当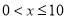 时,
时,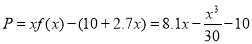
当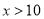 时,
时,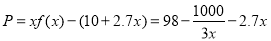

(2)①当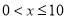 时,由
时,由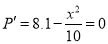 ,得
,得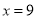 ,
,
当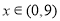 时,
时,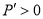 ;当
;当 时,
时,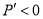 ;
;
 当
当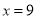 时,
时, 取最大值,且
取最大值,且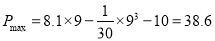
② 当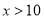 时,
时,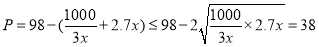
当且仅当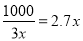 ,即
,即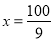 时,
时,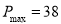
综合①、②知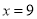 时,
时,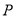 取最大值.
取最大值.
所以当年产量为9千件时,该企业生产此产品获利最大.
考点:函数及其性质的应用.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:2015届福建省高二下学期期末考理科数学试卷(解析版) 题型:选择题
箱子里有 个黑球,
个黑球,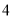 个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第
个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第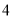 次取球之后停止的概率为
次取球之后停止的概率为
A. B.
B.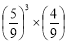 C.
C.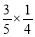 D.
D.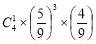
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期中考理科数学试卷(解析版) 题型:填空题
设等差数列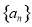 的前n项和为
的前n项和为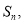 则
则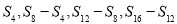 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列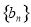 的前n项积为
的前n项积为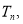 则
则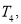 , ,
, ,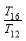 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期末考理科数学试卷(解析版) 题型:选择题
如图,正方体 ,则下列四个命题:
,则下列四个命题:
① 在直线
在直线 上运动时,三棱锥
上运动时,三棱锥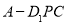 的体积不变;
的体积不变;
② 在直线
在直线 上运动时,直线
上运动时,直线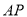 与平面
与平面 所成角的大小不变;
所成角的大小不变;
③ 在直线
在直线 上运动时,二面角
上运动时,二面角 的大小不变;
的大小不变;
④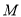 是平面
是平面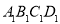 上到点D和
上到点D和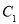 距离相等的点,则
距离相等的点,则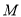 点的轨迹是过
点的轨迹是过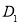 点的直线
点的直线
其中真命题的个数是

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:解答题
已知(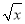 -
- )n展开式中第三项的系数比第二项的系数大162,求:
)n展开式中第三项的系数比第二项的系数大162,求:
(1) n的值;(2)展开式中含x3的项.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com