
【题目】已知函数f(x)=ax2﹣bx+lnx,(a,b∈R).
(1)若a=1,b=3,求函数f(x)的单调增区间;
(2)若b=0时,不等式f(x)≤0在[1,+∞)上恒成立,求实数a的取值范围;
(3)当a=1,b>![]() 时,记函数f(x)的导函数f
时,记函数f(x)的导函数f![]() (x)的两个零点是x1和x2(x1<x2),求证:f(x1)﹣f(x2)>
(x)的两个零点是x1和x2(x1<x2),求证:f(x1)﹣f(x2)>![]() ﹣3ln2.
﹣3ln2.
【答案】(1)f(x)在(0,![]() ),(1,+∞)递增;(2)a≤﹣
),(1,+∞)递增;(2)a≤﹣![]() ;(3)见解析
;(3)见解析
【解析】
(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题转化为a≤﹣![]() 在区间[1,+∞)恒成立,令h(x)=﹣
在区间[1,+∞)恒成立,令h(x)=﹣![]() ,根据函数的单调性求出a的范围即可;
,根据函数的单调性求出a的范围即可;
(3)由题意得x1,x2(x1<x2)是方程2x2﹣bx+1=0的两个根,记g(x)=2x2﹣bx+1,根据函数的单调性证明即可.
(1)由题意得:x>0,a=1,b=3时,f(x)=x2﹣3x+lnx,
![]() ,令f
,令f![]() (x)>0,解得:0<x<
(x)>0,解得:0<x<![]() 或x>1,
或x>1,
故f(x)在(0,![]() ),(1,+∞)递增;
),(1,+∞)递增;
(2)b=0时,f(x)=ax2+lnx,不等式f(x)≤0在[1,+∞)恒成立,
即a≤﹣![]() 在区间[1,+∞)恒成立,令h(x)=﹣
在区间[1,+∞)恒成立,令h(x)=﹣![]() ,则
,则![]() ,
,
令h![]() (x)>0,解得:x>
(x)>0,解得:x>![]() ,令h
,令h![]() (x)<0,解得:1<x<
(x)<0,解得:1<x<![]() ,
,
故f(x)在(1,![]() )递减,在(
)递减,在(![]() ,+∞)递增,故h(x)min=h(
,+∞)递增,故h(x)min=h(![]() )=﹣
)=﹣![]() ,
,
故a≤﹣![]() ;
;
(3)a=1时,f(x)=x2﹣bx+lnx,![]() ,(x>0),
,(x>0),
由题意得x1,x2(x1<x2)是方程2x2﹣bx+1=0的两个根,记g(x)=2x2﹣bx+1,则
![]() ,g(2)=9﹣2b<0,
,g(2)=9﹣2b<0,
∴x1∈(![]() ,
,![]() ),x2∈(2,+∞),且f(x)在[x1,x2]递减,
),x2∈(2,+∞),且f(x)在[x1,x2]递减,
故f(x1)﹣f(x2)>f(![]() )﹣f(2)=
)﹣f(2)=![]() ﹣3ln2,
﹣3ln2,
∵b>![]() ,∴f(x1)﹣f(x2)>
,∴f(x1)﹣f(x2)>![]() ﹣3ln2.
﹣3ln2.


科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
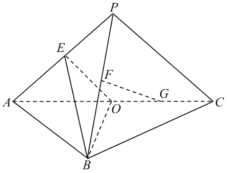
【题目】如图,在三棱锥P—ABC中,平面PAC⊥平面ABC,AB=BC,PA⊥PC.点E,F,O分别为线段PA,PB,AC的中点,点G是线段CO的中点.
(1)求证:FG∥平面EBO;
(2)求证:PA⊥BE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() ,若抛物线
,若抛物线![]() 过点
过点![]() ,且以圆0的切线为准线,
,且以圆0的切线为准线,![]() 为抛物线的焦点,点
为抛物线的焦点,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交曲线
交曲线![]() 与
与![]() 两点,
两点,![]() 关于
关于![]() 轴对称,请问:直线
轴对称,请问:直线![]() 是否过
是否过![]() 轴上的定点,如果不过请说明理由,如果过定点,请求出定点
轴上的定点,如果不过请说明理由,如果过定点,请求出定点![]() 的坐标
的坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,短轴长为![]() ,离心率为
,离心率为![]() .
.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 若过点
若过点![]() 的直线与椭圆C交于A,B两点,且P点平分线段AB,求直线AB的方程;
的直线与椭圆C交于A,B两点,且P点平分线段AB,求直线AB的方程;
![]() Ⅲ
Ⅲ![]() 一条动直线l与椭圆C交于不同两点M,N,O为坐标原点,
一条动直线l与椭圆C交于不同两点M,N,O为坐标原点,![]() 的面积为
的面积为![]() 求证:
求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.甲镇有基层干部60人,乙镇有基层干部60人,丙镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从甲、乙、丙三镇共选20名基层干部,统计他们走访贫困户的数量,并将走访数量分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5组,绘制成如图所示的频率分布直方图.
5组,绘制成如图所示的频率分布直方图.
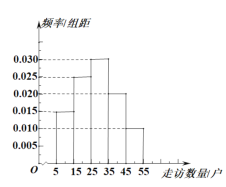
(1)求这20人中有多少人来自丙镇,并估计甲、乙、丙三镇的基层干部走访贫困户户数的中位数(精确到整数位);
(2)如果把走访贫困户达到或超过35户视为工作出色,求选出的20名基层干部中工作出色的人数,并从中选2人做交流发言,求这2人中至少有一人走访的贫困户在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com