
(1)在等差数列{an}中,已知a1=20,前n项和为Sn,且S10=S15,求当n取何值时,Sn有最大值,并求出它的最大值.
(2)已知数列{an}的通项公式是an=4n-25,求数列{|an|}的前n项和.
解:(1)由a1=20,S10=S15,解得公差d=- .
.
∵S10=S15,∴S15-S10=a11+a12+a13+a14+a15=0.
∵a11+a15=a12+a14=2a13,∴a13=0,
又∵a1>0,
∴a1、a2、…、a11、a12均为正数,而a14及以后各项均为负数.
∴当n=12或13时,Sn有最大值,为S12=S13=130.
(2)∵an=4n-25,an+1=4(n+1)-25,
∴an+1-an=4=d,又a1=4×1-25=-21.
所以数列{an}是以-21为首项,以4为公差的递增的等差数列,
令
由①得n<6 ;由②得n≥5
;由②得n≥5 ,所以n=6.
,所以n=6.
即数列{|an|}的前6项是以21为首项,公差为-4的等差数列,从第7项起以后各项构成公差为4的等差数列,
而|a7|=a7=4×7-24=3.
设{|an|}的前n项和为Tn,则



科目:高中数学 来源: 题型:
已知数列{an}中,Sn是其前n项和,若a1=1,a2=2,anan+1an+2=an+an+1+an+2,且an+1an+2≠1,则a1+a2+a3=________,S2 013=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}是以3为公差的等差数列,Sn是其前n项和,若S10是数列{Sn}中的惟一最小项,则数列{an}的首项a1的取值范围是( )
A.[-30,27] B.(30,33)
C.(-30,-27) D.[30,33]
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}的前n项和为Sn(n∈N*),关于数列{an}有下列四个命题:
①若{an}既是等差数列又是等比数列,则an=an+1(n∈N*);
②若Sn=an2+bn(a,b∈R),则{an}是等差数列;
③若Sn=1-(-1)n,则{an}是等比数列;
④若{an}是等比数列,则Sm,S2m-Sm,S3m-S2m(m∈N*)也成等比数列.
其中正确的命题是________.(填上正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知各项均为正数的数列{an}前n项和为Sn,首项为a1,且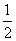 ,an,Sn成等差数列.
,an,Sn成等差数列.
(1)求数列{an}的通项公式;
(2)若a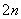 =
=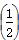 bn,设Cn=
bn,设Cn=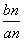 ,求数列{Cn}的前n项和Tn.
,求数列{Cn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com