
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 0.0009 | B. | 0.001 | C. | 0.009 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
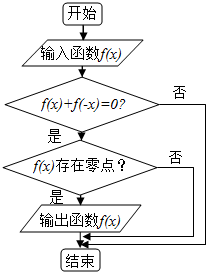 某程序据图如图所示,现输入如下四个函数:f(x)=x2,f(x)=$\frac{1}{x}$,f(x)=ex,f(x)=x3,则可以输出的函数( )
某程序据图如图所示,现输入如下四个函数:f(x)=x2,f(x)=$\frac{1}{x}$,f(x)=ex,f(x)=x3,则可以输出的函数( )| A. | f(x)=x2 | B. | f(x)=$\frac{1}{x}$ | C. | f(x)=ex | D. | f(x)=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
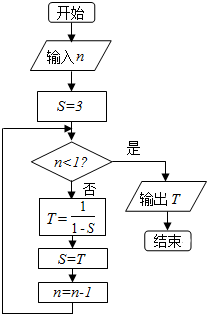
| A. | $-\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
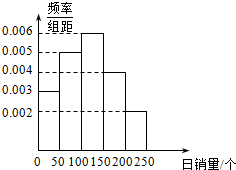 扣人心弦的2014巴西足球世界杯已落下了帷幕,德国战车再次举起大力神杯,某市足协为了解市民对该届世界杯的关注度,针对某种与世界杯有关的吉祥物的销售情况组织了一次随机调查,以下是某商店根据以往某种吉祥物的销售记录绘制的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
扣人心弦的2014巴西足球世界杯已落下了帷幕,德国战车再次举起大力神杯,某市足协为了解市民对该届世界杯的关注度,针对某种与世界杯有关的吉祥物的销售情况组织了一次随机调查,以下是某商店根据以往某种吉祥物的销售记录绘制的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 反对 | 总计 | |
| 男生 | 30 | ||
| 女生 | 25 | ||
| 总计 |
| P(K2≥k0) | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706% | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com