
已知点B(0,1),点C(0,—3),直线PB、PC都是圆 的切线(P点不在y轴上).
的切线(P点不在y轴上).
(I)求过点P且焦点在x轴上抛物线的标准方程;
(II)过点(1,0)作直线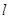 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使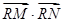 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
(I)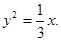 (II)存在定点R(0,0),相应的常数是
(II)存在定点R(0,0),相应的常数是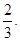
【解析】
试题分析:(I)设直线PC的方程为: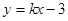 ,
,
由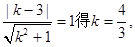 所以PC的方程为
所以PC的方程为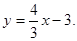
由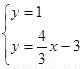 得P点的坐标为(3,1)。
得P点的坐标为(3,1)。
可求得抛物线的标准方程为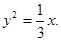
(II)设直线l的方程为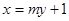 ,代入抛物线方程并整理得
,代入抛物线方程并整理得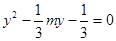
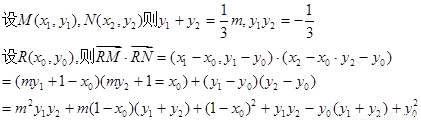
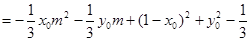 11分
11分
当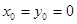 时上式是一个与m无关的常数
时上式是一个与m无关的常数
所以存在定点R(0,0),相应的常数是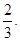
考点:直线与圆锥曲线的综合问题;平面向量数量积的运算;抛物线的标准方程.
点评:本题主要考查了直线与圆锥曲线的综合问题.研究直线与圆锥曲线位置关系的问题,通常有两种方法:一是转化为研究方程组的解的问题,利用直线方程与圆锥曲线方程所组成的方程组消去一个变量后,将交点问题(包括公共点个数、与交点坐标有关的问题)转化为一元二次方程根的问题,结合根与系数的关系及判别式解决问题;二是运用数形结合的思想.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
| RM |
| RN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 | a2 |
查看答案和解析>>
科目:高中数学 来源:安徽省蚌埠市2010年高三第三次质检数学试题(文科) 题型:解答题
已知点B(0,1),点C(0,—3),直线PB、PC都是圆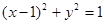 的切线(P点不在y轴上)
的切线(P点不在y轴上)
(I)求过点P且焦点在x轴上抛物线的标准方程;
(II)过点(1,0)作直线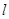 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使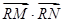 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com