
已知正方形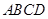 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点.
(1)在正方形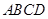 内部随机取一点
内部随机取一点 ,求满足
,求满足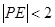 的概率;
的概率;
(2)从 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求
,求 .
.
(1)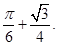
(2)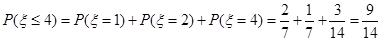
解析试题分析:解:(1)这是一个几何概型.所有点 构成的平面区域是正方形
构成的平面区域是正方形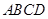 的内部,其面积是
的内部,其面积是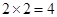 . 1分
. 1分
满足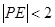 的点
的点 构成的平面区域是以
构成的平面区域是以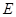 为圆心,2为半径的圆的内部与正方形
为圆心,2为半径的圆的内部与正方形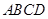 内部的公共部分,它可以看作是由一个以
内部的公共部分,它可以看作是由一个以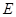 为圆心、2为半径、圆心角为
为圆心、2为半径、圆心角为 的扇形的内部与两个直角边分别为1和
的扇形的内部与两个直角边分别为1和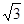 的直角三角形内部构成. 2分
的直角三角形内部构成. 2分
其面积是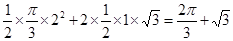 . 4分
. 4分
所以满足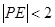 的概率为
的概率为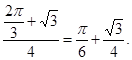 5分
5分
(2)从 这八个点中,任意选取两个点,共可构成
这八个点中,任意选取两个点,共可构成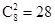 条不同的线段. 6分
条不同的线段. 6分
其中长度为1的线段有8条,长度为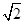 的线段有4条,长度为2的线段有6条,长度为
的线段有4条,长度为2的线段有6条,长度为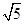 的线段有8条,长度为
的线段有8条,长度为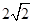 的线段有2条.所以
的线段有2条.所以 所有可能的取值为
所有可能的取值为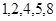 . 7分
. 7分
且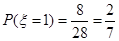 ,
, 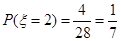 ,
, 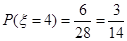
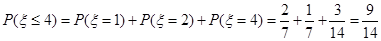 . 12分
. 12分
考点:古典概型的概率
点评:主要是考查了古典概型的概率的求解运用,属于基础题。


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
某学校篮球队、羽毛球队、乒乓球队的某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某部门对当地城乡居民进行了主题为“你幸福吗?”的幸福指数问卷调査,并在已被问卷调查的居民中随机抽选部分居民参加“幸福职业”或“幸福愿景”的座谈会,被邀请的居民只能选择其中一场座谈会参加.已知A小区有1人,B小区有3人收到邀请并将参加一场座谈会,若A小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是 , B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是
, B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是 .
.
(Ⅰ)求A、B两个小区已收到邀请的人选择“幸福愿景”座谈会的人数相等的概率;
(Ⅱ)在参加“幸福愿景”座谈会的人中,记A、B两个小区参会人数的和为 ,试求
,试求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为了推动全民健身运动在全市的广泛开展,该市电视台开办了健身竞技类栏目《健身大闯关》,规定参赛者单人闯关,参赛者之间相互没有影响,通过关卡者即可获奖。现有甲、乙、丙 人参加当天的闯关比赛,已知甲获奖的概率为
人参加当天的闯关比赛,已知甲获奖的概率为 ,乙获奖的概率为
,乙获奖的概率为 ,丙获奖而甲没有获奖的概率为
,丙获奖而甲没有获奖的概率为 。
。
(Ⅰ)求三人中恰有一人获奖的概率;
(Ⅱ)求三人中至少有两人获奖的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校在2011年的自主招生考试成绩中随机抽取 100名学生的笔试成绩,按成绩分组,得到的频率分布表如下所示.
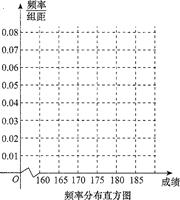
(1)请先求出频率分布表中①,②位置相应的数据,再完成下列频率分布直方图;并确定中位数。(结果保留2位小数)
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的条件下,学校决定在6名学生中随机抽取2名学生接受考官进行面试,求第4组至少有一名学生被考官A面试的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一个盒子中,放有标号分别为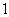 ,
,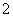 ,
,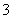 的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为
的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为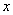 、
、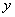 ,设
,设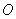 为坐标原点,设
为坐标原点,设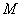 的坐标为
的坐标为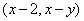 .
.
(1)求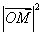 的所有取值之和;
的所有取值之和;
(2)求事件“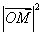 取得最大值”的概率.
取得最大值”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种家用电器每台的销售利润与该电器的无故障时间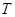 (单位:年)有关,若
(单位:年)有关,若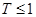 ,则销售利润为0元;若
,则销售利润为0元;若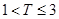 ,则销售利润为100元,若
,则销售利润为100元,若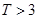 ,则销售利润为200元.设每台该种电器的无故障使用时间
,则销售利润为200元.设每台该种电器的无故障使用时间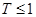 ,
,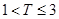 ,
,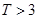 这三种情况发生的概率分别为
这三种情况发生的概率分别为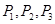 ,又知
,又知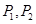 为方程
为方程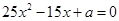 的两根,且
的两根,且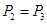 .
.
(1)求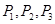 的值;
的值;
(2)记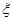 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求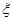 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com