
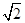 ,b在a方向上的投影为
,b在a方向上的投影为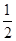 ,(a-c)·(b-c)=0,则|c|的最大值是________.
,(a-c)·(b-c)=0,则|c|的最大值是________. 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源:不详 题型:解答题
 b,m∈R,k、t为正实数.
b,m∈R,k、t为正实数.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
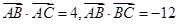 则
则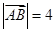 ;
;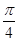
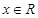 ,都有sinx≤1,则
,都有sinx≤1,则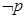 为:存在
为:存在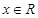 ,使得sinx > 1.
,使得sinx > 1.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ;③若△ABC中,a="5,b=8," c=7,则
;③若△ABC中,a="5,b=8," c=7,则 ·
· =20;④若非零向量a,b满足|a+b|=|b|,则|2b|>|a+2b|.其中所有真命题的序号是 .
=20;④若非零向量a,b满足|a+b|=|b|,则|2b|>|a+2b|.其中所有真命题的序号是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
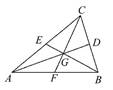
A. = =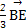 |
B.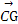 =2 =2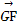 |
C.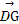 = = |
D.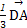 + + = =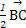 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com