
| A. | -1 | B. | -3 | C. | $-\frac{1}{3}$ | D. | 1 |
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
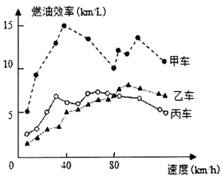 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )| A. | 消耗1升汽油,乙车最多可行驶5千米 | |
| B. | 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多 | |
| C. | 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油 | |
| D. | 甲车以80千米/小时的速度行驶1小时,消耗10升汽油 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (1,0) | C. | (1,2) | D. | (0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{7}{5}$ | C. | $\frac{14}{5}$ | D. | $-\frac{2}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com