
【题目】如图,已知平行四边形![]() 和矩形
和矩形![]() 所在平面垂直,其中
所在平面垂直,其中![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)若点![]() 到平面
到平面![]() 的距离是
的距离是![]() ,求多面体
,求多面体![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)首先连接![]() ,
,![]() ,根据面面垂直的性质得到
,根据面面垂直的性质得到![]() 平面
平面![]() ,根据线面垂直的性质得到
,根据线面垂直的性质得到![]() .根据
.根据![]() 可得到
可得到![]() ,再根据线面垂直的判定即可证明
,再根据线面垂直的判定即可证明![]() 平面
平面![]() ,即证
,即证![]() .
.
(2)首先取![]() 中点
中点![]() ,连接
,连接![]() ,根据
,根据![]() 平面
平面![]() 得到点
得到点![]() 到平面
到平面![]() 的距离就是
的距离就是![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,利用面面垂直的性质即可证明
,利用面面垂直的性质即可证明![]() 为三棱柱
为三棱柱![]() 的高,再求其体积即可.
的高,再求其体积即可.
(1)连接![]() ,因为
,因为![]() 为正三角形,
为正三角形,![]() 为棱
为棱![]() 的中点,
的中点,

所以![]() ,因为
,因为![]() ,从而
,从而![]() ,
,
又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() .①
.①
设![]() ,所以
,所以![]() ,
,![]()
又![]() ,所以
,所以![]() ,
,
所以![]() .
.
又![]() ,所以
,所以![]() .
.
则![]() ,②
,②
由①②及![]() ,可得
,可得![]() 平面
平面![]() .
.
所以![]() .
.
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
则![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
故点![]() 到平面
到平面![]() 的距离就是点
的距离就是点![]() 到平面
到平面![]() 的距离
的距离![]() .
.
故![]() ,因
,因![]() ,得
,得![]() ,则
,则![]() ,
,
取![]() 中点
中点![]() ,连接
,连接![]() ,因为
,因为![]() 为正三角形,所以
为正三角形,所以![]() .
.
因为平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() .
.
所以![]()
![]() 平面
平面![]() ,
,
所以![]() 为三棱柱
为三棱柱![]() 的高
的高![]() ,
,
由已知可得,![]() ,
,
所以三棱柱![]() 的体积
的体积![]() .
.


科目:高中数学 来源: 题型:
【题目】为发挥体育咋核心素养时代的独特育人价值,越来越多的中学生已将某些体育项目纳入到学生的必修课程,某中学计划在高一年级开设游泳课程,为了解学生对游泳的兴趣,某数学研究学习小组随机从该校高一年级学生抽取了100人进行调查.
班 级 | 一(1) | 一(2) | 一(3) | 一(4) | 一(5) | 一(6) | 一(7) | 一(8) | 一(9) | 一(10) |
市级比赛 获奖人数 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 2 |
市级以上比 赛获奖人数 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 2 | 1 | 2 |
(1)已知在被抽取的女生中有6名高一(1)班学生,其中3名对游泳有兴趣,现在从这6名学生中最忌抽取3人,求至少有2人对游泳有兴趣的概率;
(2)该研究性学习小组在调查发现,对游泳有兴趣的学生中有部分曾在市级以上游泳比赛中获奖,如上表所示,若从高一(8)班和高一(9)班获奖学生中随机各抽取2人进行跟踪调查.记选中的4人中市级以上游泳比赛获奖的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
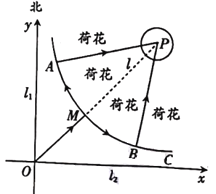
【题目】如图,某市建有贯穿东西和南北的两条垂直公路![]() ,
,![]() ,在它们交叉路口点
,在它们交叉路口点![]() 处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台
处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台![]() 位于两条垂直公路的角平分线
位于两条垂直公路的角平分线![]() 上,
上,![]() 与环形公路的交点记作
与环形公路的交点记作![]() .游客游览荷花池时,需沿公路
.游客游览荷花池时,需沿公路![]() 先到达环形公路
先到达环形公路![]() 处.为了分流游客,方便游客游览荷花池,计划从靠近公路
处.为了分流游客,方便游客游览荷花池,计划从靠近公路![]() ,
,![]() 的环形公路上选
的环形公路上选![]() ,
,![]() 两处(
两处(![]() ,
,![]() 关于直线
关于直线![]() 对称)修建直达观景台
对称)修建直达观景台![]() 的玻璃栈道
的玻璃栈道![]() ,
,![]() .以
.以![]() ,
,![]() 所在的直线为
所在的直线为![]() ,
,![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,靠近公路
,靠近公路![]() ,
,![]() 的环形公路可用曲线
的环形公路可用曲线![]() 近似表示,曲线
近似表示,曲线![]() 符合函数
符合函数![]() .
.
(1)若![]() 百米,点
百米,点![]() 到
到![]() 的垂直距离为1百米,求玻璃栈道
的垂直距离为1百米,求玻璃栈道![]() 的总长度;
的总长度;
(2)若要使得玻璃栈道![]() 的总长度最小为
的总长度最小为![]() 百米,求观景台
百米,求观景台![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,其焦点为
,其焦点为![]() ,直线
,直线![]() 过点
过点![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,当
两点,当![]() 的斜率为
的斜率为![]() 时,
时,![]() .
.
(1)求![]() 的值;
的值;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() 满足
满足![]() (点
(点![]() 为坐标原点)?若存在,求
为坐标原点)?若存在,求![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Serum Drug Concentration)是指药物吸收后在血浆内的总浓度(单位:mg/ml),通常用血药浓度来研究药物的作用强度.下图为服用同等剂量的三种新药后血药浓度的变化情况,其中点![]() 的横坐标表示服用第
的横坐标表示服用第![]() 种药后血药浓度达到峰值时所用的时间,其它点的横坐标分别表示服用三种新药后血药浓度第二次达到峰值一半时所用的时间(单位:h),点
种药后血药浓度达到峰值时所用的时间,其它点的横坐标分别表示服用三种新药后血药浓度第二次达到峰值一半时所用的时间(单位:h),点![]() 的纵坐标表示第
的纵坐标表示第![]() 种药的血药浓度的峰值.(
种药的血药浓度的峰值.(![]() )
)

①记![]() 为服用第
为服用第![]() 种药后达到血药浓度峰值时,血药浓度提高的平均速度,则
种药后达到血药浓度峰值时,血药浓度提高的平均速度,则![]() 中最大的是_______;
中最大的是_______;
②记![]() 为服用第
为服用第![]() 种药后血药浓度从峰值降到峰值的一半所用的时间,则
种药后血药浓度从峰值降到峰值的一半所用的时间,则![]() 中最大的是_______
中最大的是_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且与直线
,且与直线![]() 相切,椭圆
相切,椭圆![]() 的对称轴为坐标轴,
的对称轴为坐标轴,![]() 点为坐标原点,
点为坐标原点,![]() 是其一个焦点,又点
是其一个焦点,又点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的标准方程和椭圆
的标准方程和椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的动直线
的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 点,交轨迹
点,交轨迹![]() 于
于![]() 两点,设
两点,设![]() 为
为![]() 的面积,
的面积,![]() 为
为![]() 的面积,令
的面积,令![]() 的面积,令
的面积,令![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点![]() 的轨迹
的轨迹![]() 的标准方程;
的标准方程;
(2)设动直线![]() 与曲线
与曲线![]() 有且仅有一个公共点,与圆
有且仅有一个公共点,与圆![]() 相交于两点
相交于两点![]() (两点均不在坐标轴上),求直线
(两点均不在坐标轴上),求直线![]() 的斜率之积.
的斜率之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com