
已知数列{an}的前n项和为Sn,且Sn=2an-2(n∈N*),在数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上.
(1)求数列{an},{bn}的通项公式;
(2)记Tn=a1b1+a2b2+ +anbn,求Tn.
(1)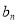 =2n-1;(2)
=2n-1;(2)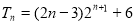 .
.
【解析】
试题分析:(1)利用“当n=1,a1=2;当n≥2时,an=Sn-Sn-1”和等比数列的通项公式即可得出an;利用等差数列的定义和通项公式即可得出bn.
(Ⅱ)先把所求结论代入求出数列{cn}的通项,再利用数列求和的错位相减法即可求出其各项的和.
试题解析:解(1)由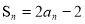 ,得
,得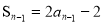 (n≥2)
(n≥2)
两式相减得 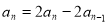 即
即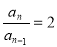 (n≥2)
(n≥2)
又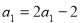 ,∴
,∴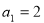
∴{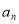 }是以2为首项,以2为公比的等比数列 ∴
}是以2为首项,以2为公比的等比数列 ∴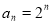
∵点P( 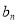 ,
,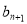 )在直线x-y+2=0上
)在直线x-y+2=0上
∴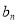 -
- 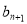 +2=0 即
+2=0 即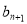 -
-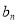 =2
=2
∴{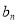 }是等差数列,∵
}是等差数列,∵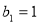 ∴
∴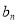 =2n-1
=2n-1
(2) ∵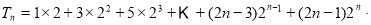
∴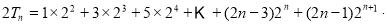
两式相减得,
-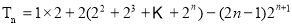
=2+2·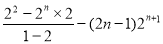
=2+4·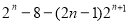
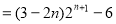
∴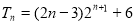
考点:1.数列的求和;2.等比数列;3.数列递推式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016届安徽省高一第二学期第一次月考数学试卷(解析版) 题型:选择题
将某选手的7个得分去掉1个最高分,去掉1个最低分,剩余5个得分的平均分为91,现场做的7个得分的茎叶图(如图)后来有一个数据模糊,无法辨认,在图中用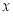 表示,则x的值为( )
表示,则x的值为( )
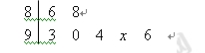
A.0 B.4 C.5 D.7
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期末考试数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,直线3x+4y-5=0与圆x2+y2=4相交于A,B两点,则弦AB的长等于 。
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期末考试数学试卷(解析版) 题型:选择题
在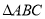 中,已知
中,已知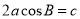 ,
, 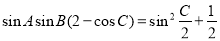 ,则
,则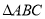 为( )
为( )
A.等边三角形 B.等腰直角三角形
C.锐角非等边三角形 D.钝角三角形
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期中考试数学试卷(解析版) 题型:填空题
对于问题:“已知关于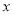 的不等式
的不等式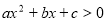 的解集为(-1,2),解关于
的解集为(-1,2),解关于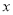 的不等式
的不等式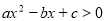 ”,给出如下一种解法:
”,给出如下一种解法:
【解析】
由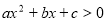 的解集为(-1,2),得
的解集为(-1,2),得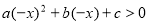 的解集为(-2,1),
的解集为(-2,1),
即关于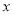 的不等式
的不等式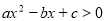 的解集为(-2,1)
的解集为(-2,1)
参考上述解法,若关于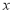 的不等式
的不等式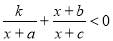 的解集为(-1,
的解集为(-1, 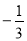 )
) (
(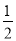 ,1),则关于
,1),则关于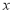 的不等式
的不等式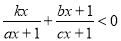 的解集为________________
的解集为________________
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期中考试数学试卷(解析版) 题型:选择题
在△ABC中,若lg sin A-lg cos B-lg sin C=lg 2,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源:2016届安徽省安庆市外国语学校高一下学期期中考试数学试卷(解析版) 题型:填空题
若数列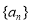 的前
的前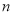 项和
项和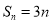 ,则此数列的通项公式为____________________.
,则此数列的通项公式为____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com