在平面直角坐标系xOy中,抛物线C的焦点在y轴上,且抛物线上的点P(x,4)到焦点F的距离为5.斜率为2的直线l与抛物线C交于A,B两点.
(Ⅰ)求抛物线C的标准方程,及抛物线在P点处的切线方程;
(Ⅱ)若AB的垂直平分线分别交y轴和抛物线于M,N两点(M,N位于直线l两侧),当四边形AMBN为菱形时,求直线l的方程.
【答案】
分析:(Ⅰ)设抛物线的方程,根据点P到焦点F的距离为5,可得抛物线的标准方程,利用导数,即可求得抛物线在P点处的切线方程;
(Ⅱ)设直线l的方程与抛物线方程联立,利用韦达定理,求得AB的中点,从而可得AB的垂直平分线方程,进一步确定M、N的坐标,即可求得直线l的方程.
解答:解:(Ⅰ)依题意设抛物线C:x
2=2py(p>0),
因为点P到焦点F的距离为5,所以点P到准线
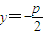
的距离为5.
因为P(x
,4),所以由抛物线准线方程可得
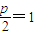
,∴p=2.
所以抛物线的标准方程为x
2=4y. …(4分)
即
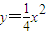
,所以
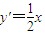
,点P(±4,4),
所以
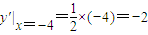
,
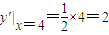
.
所以点P(-4,4)处抛物线切线方程为y-4=-2(x+4),即2x+y+4=0;点P(4,4)处抛物线切线方程为y-4=2(x-4),即2x-y-4=0.
所以P点处抛物线切线方程为2x+y+4=0,或2x-y-4=0. …(7分)
(Ⅱ)设直线l的方程为y=2x+m,A(x
1,y
1),B(x
2,y
2),
联立
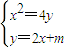
,消y得x
2-8x-4m=0,△=64+16m>0.
所以x
1+x
2=8,x
1x
2=-4m,
所以
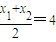
,

,
即AB的中点为Q(4,8+m).
所以AB的垂直平分线方程为

.
因为四边形AMBN为菱形,所以M(0,m+10),
因为M,N关于Q(4,8+m)对称,所以N点坐标为N(8,m+6),
因为N在抛物线上,所以64=4×(m+6),即m=10,
所以直线l的方程为y=2x+10. …(14分)
点评:本题考查抛物线的标准方程,考查抛物线的切线方程,考查直线与抛物线的位置关系,考查韦达定理的而运用,考查学生的计算能力,属于中档题.

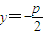 的距离为5.
的距离为5.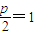 ,∴p=2.
,∴p=2.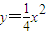 ,所以
,所以 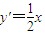 ,点P(±4,4),
,点P(±4,4),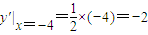 ,
,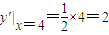 .
.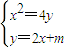 ,消y得x2-8x-4m=0,△=64+16m>0.
,消y得x2-8x-4m=0,△=64+16m>0.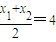 ,
, ,
, .
.

 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是