练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．设函数f（x）的定义域为R，若存在常数m＞0，使|f（x）|≤m|x|对一切实数x均成立，则称f（x）为“倍约束函数”．现给出下列函数：①f（x）=0；②f（x）=x2；③f（x）=$\frac{x}{{x}^{2}+x+1}$；④f（x）是定义在实数集R上的奇函数，且对一切x1，x2均有|f（x1）-f（x2）|≤2|x1-x2|．其中是“倍约束函数”的序号是（　　）
    A．①②④B．③④C．①④D．①③④

    分析 本题考查阅读题意的能力，根据F函数的定义对各选项进行判定．比较各个选项，发现只有选项①③④，根据单调性可求出存在正常数M满足条件，而对于其它选项，不等式变形之后，发现都不存在正常数M使之满足条件，由此即可得到正确答案．

    解答 解：对于①，m是任意正数时都有0≤m|x|，f（x）=0是F函数，故①正确；
    对于②，f（x）=x2，|f（x）|=|x2|≤m|x|，即|x|≤m，不存在这样的M对一切实数x均成立，故②错；
    对于③，要使|f（x）|≤m|x|成立，即|$\frac{x}{{x}^{2}+x+1}$|≤m|x|，当x=0时，m可取任意正数；当x≠0时，只须m$≥（\frac{1}{{x}^{2}+x+1}）_{max}$，因为x2+x+1$≥\frac{3}{4}$，∴所以m≥$\frac{4}{3}$故③正确．
    对于④，f（x）是定义在实数集R上的奇函数，故|f（x）|是偶函数，因而由|f（x1）-f（x2）|≤2|x1-x2|得到，|f（x）|≤2|x|成立，存在M≥2＞0，使|f（x）|≤M|x|对一切实数x均成立，符合题意，故④正确．
    故选：D．

    点评 本题重点考查了函数的最值及其性质，对选支逐个加以分析变形，利用函数、不等式的进行检验，方可得出正确结论．深刻理解题中F函数的定义，用不等式的性质加以处理，找出不等式恒成立的条件再进行判断，是解决本题的关键所在，属于难题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．f（x）=x•ex-1的零点个数为1个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

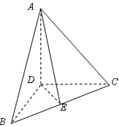    12．如图，在三棱锥A-BCD中，DA，DB，DC两两垂直，且DB=DC，E为BC中点，则$\overrightarrow{AE}•\overrightarrow{BC}$=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．函数$y=\sqrt{（x-1）（x-2）}+\sqrt{x-1}$的定义域为{x︳x=1或x≥2}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知数列{an}是等差数列，a1=1，a3=5，则公差d等于（　　）
    A．-2B．-1C．2D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知g（x）=f（x）+|x-1|是奇函数，且f（-1）=1，则g（1）=-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设全集U={2，4，-（a-3）2}，集合A={2，a2-a+2}，若∁UA={-1}，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知点F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，点E是该双曲线的右焦点，过点F且垂直于x轴的直线与双曲线相交于A，B两点，若$\overrightarrow{EA}$•$\overrightarrow{EB}$＞0，则该双曲线的离心率e的取值范围是（　　）
    A．（$\sqrt{2}$，+∞）B．（1，$\sqrt{2}$+1）C．（2，+∞）D．（1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知圆C：x2+（y-4）2=r2，直线l过点M（-2，0）
    （Ⅰ）若圆C的半径r=2，直线l与圆C相切，求直线l的方程；
    （Ⅱ）若直线l的倾斜角α=135°，且直线l与圆C相交于A、B两点，弦长$|{AB}|=2\sqrt{2}$，求圆C的方程．

    查看答案和解析>>

    同步练习册答案