
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\sqrt{2}$+1) | C. | (2,+∞) | D. | (1,2) |
分析 要使$\overrightarrow{EA}•\overrightarrow{EB}>0$,只需满足∠AEB为锐角,只需满足∠AEF<45°,即|AF|<|EF|,将此式转化为关于a、c的不等式,化简整理即可得到该双曲线的离心率e的取值范围.
解答 解:要使$\overrightarrow{EA}•\overrightarrow{EB}>0$,只需满足∠AEB为锐角,只需满足∠AEF<45°.
在△AEF中,$tan∠AEF=\frac{{|{AE}|}}{{|{EF}|}}=\frac{{\frac{b^2}{a}}}{a+c}<1$,即c2-ac-2a2<0,两边同除以a2,e2-e-2<0,
又e>1,
所以离心率e的取值范围是(1,2).
故选:D.
点评 本题考查双曲线离心率的范围,着重考查了双曲线的标准方程与简单几何性质等知识,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
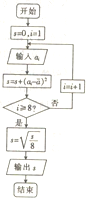 一天中对某人的心跳检测了8次,得到如表所示的数据
一天中对某人的心跳检测了8次,得到如表所示的数据| 检测次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 检测数据a(次/分钟) | 59 | 60 | 62 | 62 | 63 | 65 | 66 | 67 |
| A. | $\sqrt{7}$ | B. | 7 | C. | 8 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ③④ | C. | ①④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{3}$或-$\frac{3}{5}$ | B. | -$\frac{3}{2}$或-$\frac{2}{3}$ | C. | -$\frac{5}{4}$或-$\frac{4}{5}$ | D. | -$\frac{4}{3}$或-$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N={ 4,6 } | B. | M∪N=U | C. | (∁UN )∪M=U | D. | (∁UM)∩N=N |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com