
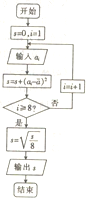
 一天中对某人的心跳检测了8次,得到如表所示的数据
一天中对某人的心跳检测了8次,得到如表所示的数据| 检测次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 检测数据a(次/分钟) | 59 | 60 | 62 | 62 | 63 | 65 | 66 | 67 |
| A. | $\sqrt{7}$ | B. | 7 | C. | 8 | D. | 2$\sqrt{2}$ |
分析 由题意及程序框图知,该程序框图的功能是输出这8个数据的方差,由公式结合题设中的数据计算出方差,选出正确选项即可得解.
解答 解:该程序是计算这八个数的标准差,
其中$\overline{a}$=$\frac{59+60+62+62+63+65+66+67}{8}$=63,
循环结束时,
s=(59-63)2+(60-63)2+(62-63)2+(62-63)2+(63-63)2+(65-63)2+(66-63)2+(67-63)2
=16+9+1+1+0+4+9+16
=56.
则输出的值为$\sqrt{\frac{56}{8}}$=$\sqrt{7}$.
故选:A.
点评 本题考查循环结构,理解题意,由框图得出本题所研究问题的算法是解题的关键,框图的考查是近几年的高考必考题,其与高中阶段所学的多种知识结合,考查知识点比较宽泛,本题结合的比较新颖,平时应注意总结框图与其它知识相结合考查的方式,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a^{\frac{1}{3}}}$ | B. | ${a^{\frac{3}{2}}}$ | C. | ${a^{\frac{2}{3}}}$ | D. | ${a^{\frac{1}{6}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2-\sqrt{3}}}{2}$ | B. | $\frac{{2-\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}-1}}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
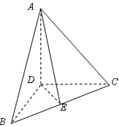 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC,E为BC中点,则$\overrightarrow{AE}•\overrightarrow{BC}$=0.
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC,E为BC中点,则$\overrightarrow{AE}•\overrightarrow{BC}$=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\sqrt{2}$+1) | C. | (2,+∞) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com